题目内容
1.对实数列{an},若存在常数M>0,使得对任意的n∈N*,|an|≤M,(*),则称数列{an}为有界数列,若M是使(*)成立的最小正常数,则称M是最佳上界,现定义:ak=$\frac{1}{{k}^{2}}$+$\frac{1}{{k}^{2}+1}$+…+$\frac{1}{(k+1)^{2}-1}$(k=1,2,…).(1)比较a1,a2,a3的大小,并猜想数列{an}的单调性(不需证明);
(2)定义数列{an}的交替和为:Sn=a1-a2+a3-a4+…+(-1)n-1an,问:数列{Sn}是否为有界函数?证明你的结论;
(3)①(理科)证明:数列{nan}为有界数列,并求此数列的最佳上界M;
②(文科)证明:数列{nan}为有界数列.
分析 (1)a1=$\frac{1}{{1}^{2}}+\frac{1}{{1}^{2}+1}+\frac{1}{{2}^{2}-1}$=$1+\frac{1}{2}+\frac{1}{3}$,同理可得a2=$\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}$+$\frac{1}{8}$,a3=$\frac{1}{9}+\frac{1}{10}$+…+$\frac{1}{15}$,猜想数列{an}的单调递减.
(2)当n=2k(k∈N*)时,Sn=(a1-a2)+(a3-a4)+…+(a2k-1-a2k),由于a2k-1-a2k>0,因此n→+∞时,Sn→+∞,为无界函数.当n=2k-1(k∈N*)时,Sn=a1-a2+a3-a4+…+(-1)n-1an=(a1-a2)+(a3-a4)+…+(a2k-3-a2k-1)+a2k-1,同样为无界函数.
(3)①(理科)证明:kak=$\frac{k}{{k}^{2}}$+$\frac{k}{{k}^{2}+1}$+…+$\frac{k}{(k+1)^{2}-1}$,$\frac{k}{{k}^{2}+m}$=$\frac{1}{k+\frac{m}{k}}$≤$\frac{1}{2\sqrt{m}}$,可得nan≤$\frac{1}{n}$+$\frac{1}{2\sqrt{1}}$+$\frac{1}{2\sqrt{2}}$+…+$\frac{1}{2\sqrt{2n}}$<$\sqrt{2n}$+1,数列{nan}为有界数列,利用数学归纳法证明:$1+\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{2n}}$<$2\sqrt{2n}$即可.
解答 (1)解:a1=$\frac{1}{{1}^{2}}+\frac{1}{{1}^{2}+1}+\frac{1}{{2}^{2}-1}$=$1+\frac{1}{2}+\frac{1}{3}$,
a2=$\frac{1}{{2}^{2}}+\frac{1}{{2}^{2}+1}$+$\frac{1}{{2}^{2}+2}$+$\frac{1}{{2}^{2}+3}$+$\frac{1}{{3}^{2}-1}$=$\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}$+$\frac{1}{8}$<a1,
a3=$\frac{1}{{3}^{2}}+\frac{1}{{3}^{2}+1}$+$\frac{1}{{3}^{2}+2}$+…+$\frac{1}{{4}^{2}-1}$=$\frac{1}{9}+\frac{1}{10}$+…+$\frac{1}{15}$<a2,
猜想数列{an}的单调递减.
(2)解:当n=2k(k∈N*)时,Sn=a1-a2+a3-a4+…+(-1)n-1an=(a1-a2)+(a3-a4)+…+(a2k-1-a2k)
由于a2k-1-a2k>0,因此n→+∞时,Sn→+∞,为无界函数.
当n=2k-1(k∈N*)时,Sn=a1-a2+a3-a4+…+(-1)n-1an=(a1-a2)+(a3-a4)+…+(a2k-3-a2k-1)+a2k-1,同样为无界函数.
因此数列{Sn}是否为有界函数.
(3))①(理科)证明:kak=$\frac{k}{{k}^{2}}$+$\frac{k}{{k}^{2}+1}$+…+$\frac{k}{(k+1)^{2}-1}$,$\frac{k}{{k}^{2}+m}$=$\frac{1}{k+\frac{m}{k}}$≤$\frac{1}{2\sqrt{m}}$,
∴nan≤$\frac{1}{n}$+$\frac{1}{2\sqrt{1}}$+$\frac{1}{2\sqrt{2}}$+…+$\frac{1}{2\sqrt{2n}}$<$\sqrt{2n}$+1,数列{nan}为有界数列,
下面利用数学归纳法证明:$1+\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{2n}}$<$2\sqrt{2n}$.
(i)当n=1时,左边=1+$\frac{1}{\sqrt{2}}$<2$\sqrt{2}$,成立.
(ii)假设当n=k∈N*时,$1+\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{2k}}$<2$\sqrt{2k}$.
则当n=k+1时,左边=$1+\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{2k}}$+$\frac{1}{\sqrt{2k+1}}$+$\frac{1}{\sqrt{2k+2}}$<2$\sqrt{2k}$+$\frac{1}{\sqrt{2k+1}}$+$\frac{1}{\sqrt{2k+2}}$,
下面证明:2$\sqrt{2k}$+$\frac{1}{\sqrt{2k+1}}$+$\frac{1}{\sqrt{2k+2}}$<2$\sqrt{2k+2}$,即证明$\frac{1}{\sqrt{2k+1}}$+$\frac{1}{\sqrt{2k+2}}$<$\frac{4}{\sqrt{2k+2}+\sqrt{2k}}$.
此数列的最佳上界M=$\sqrt{2n}$+1.
点评 本题考查了数列的递推关系、数学归纳法、不等式的性质,考查了推理能力与计算能力,属于难题.

 名校课堂系列答案
名校课堂系列答案| A. | 1 | B. | -1 | C. | 2 | D. | 0 |
| A. | 总有MP+OM>1 | B. | 总有MP+OM=1 | ||
| C. | 存在角α,使MP+OM=1 | D. | 不存在角α,使MP+OM<0 |
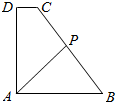 如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.
如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.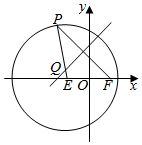 如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.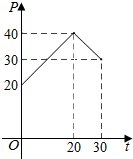 据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.
据市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t (t∈N)(天)的关系如图所示.