题目内容
18.设函数f(x)=-x2+2x+3,x∈(-3,2],则f(x)的值域为( )| A. | (-12,3] | B. | (-12,3) | C. | (-12,4] | D. | (-12,4) |
分析 配方可得,f(x)=-(x-1)2+4,函数的对称轴为直线x=1,确定函数在(-3,1)上单调增,在(1,2]上单调减,从而可求函数的值域.
解答 解:配方可得,f(x)=-(x-1)2+4,函数的对称轴为直线x=1
∴函数在(-3,1)上单调增,在(1,2]上单调减,
∵x=1时,f(1)=4;x=-3时,f(-3)=-12
∴函数f(x)的值域为(-12,4]
故选:C.
点评 本题考查二次函数的最值,解题的关键是配方,确定函数的单调性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.函数y=x2+x+1的极小值是( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{7}{4}$ | D. | 不存在 |
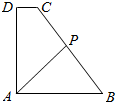 如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.
如图,直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AD}$(m,n均为正实数),则$\frac{1}{m}+\frac{1}{n}$的最小值为$\frac{7+4\sqrt{3}}{4}$.