题目内容
已知等差数列{an},其前n项和为Sn,若S4=4S2,a2n=2an+1
(1)求数列{an}的通项公式;
(2)对任意m∈N*,将数列{an}中落入区间(2m,2m+1)内的项的个数记为{bm}
①求数列{bm}的通项公式;
②记cm=
,数列{cm}的前m项和为Tm,求所有使得等式
=
的正整数m,t.
(1)求数列{an}的通项公式;
(2)对任意m∈N*,将数列{an}中落入区间(2m,2m+1)内的项的个数记为{bm}
①求数列{bm}的通项公式;
②记cm=
| 2 |
| 22m-1-bm |
| Tm-t |
| Tm+1-t |
| 1 |
| ct+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据等差数列的性质列方法求解a1=1,d=2,即可得出通项公式.(2)求解2n-1>2m,2n-1<22m,得出2m-1+
<n<22m-1+
,即可得出项数bm
(3)求出{cn}通项公式,前n项和,再代入求解即可.
| 1 |
| 2 |
| 1 |
| 2 |
(3)求出{cn}通项公式,前n项和,再代入求解即可.
解答:
解:(1)∵等差数列{an},其前n项和为Sn,若S4=4S2,a2n=2an+1,
∴4a1-2d=0,a1=d-1,∴a1=1,d=2,
∴an=2n-1
(2)∵an=2n-1,
∴2n-1>2m,2n-1<22m,
∴2m-1+
<n<22m-1+
,
即项数22m-1-2m-1,
∴①bm=22m-1-2m-1
∵cm=
,
∴Cm=
,
∴c1=2,
=
,
∴{cn}是等比数列,数列{cm}的前m项和为Tm=
即Tm=4(1-
),
∵所有使得等式
=
∴(4-t)2m=4+2t-1
存在符合条件的正整数m=t=3,
∴4a1-2d=0,a1=d-1,∴a1=1,d=2,
∴an=2n-1
(2)∵an=2n-1,
∴2n-1>2m,2n-1<22m,
∴2m-1+
| 1 |
| 2 |
| 1 |
| 2 |
即项数22m-1-2m-1,
∴①bm=22m-1-2m-1
∵cm=
| 2 |
| 22m-1-bm |
∴Cm=
| 2 |
| 2m-1 |
∴c1=2,
| Cn+1 |
| Cn |
| 1 |
| 2 |
∴{cn}是等比数列,数列{cm}的前m项和为Tm=
2(1-(
| ||
1-
|
即Tm=4(1-
| 1 |
| 2m |
∵所有使得等式
| Tm-t |
| Tm+1-t |
| 1 |
| ct+1 |
∴(4-t)2m=4+2t-1
存在符合条件的正整数m=t=3,
点评:本题综合考察了数列的性质,几何不等式等知识,运算思维量大,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=(
)x-
的图象可能是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、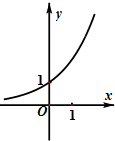 |
B、 |
C、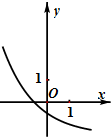 |
D、 |
阅读如图程序框图,下列说法正确的是( )
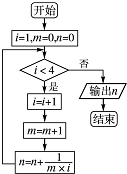

| A、该框图只含有顺序结构、条件结构 |
| B、该框图只含有顺序结构、循环结构 |
| C、该框图只含有条件结构、循环结构 |
| D、该框图包含顺序结构、条件结构、循环结构 |