Question

三棱台ABC-A′B′C′的两底面是等边三角形且边长之比是2：1，连接A′C，B′C，A′B把棱台分为三个棱锥，则有
V_{C′-A′B′C}：V_B′-A′BC：V_A′-ABC=

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：画出图形，结合图形，设棱台的高为h，△A′B′C′的面积为S，求出各三棱锥的体积即可．

解答： 解：画出图形，如图所示，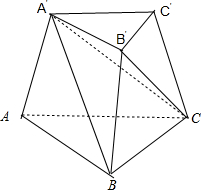
由题意，设棱台的高为h，△A′B′C′的面积为S；
∴VA′-ABC=

1

3

S_△ABCh=

4

3

Sh；
VB-A′B′C′=

1

3

S_△A'B'C'h=

1

3

Sh；
VA′-B′BC=V_总-VA′-ABC-VC-A′B′C′
=

1

3

（4S+

4S•S

+S）h-

4

3

Sh-

1

3

Sh=

2

3

Sh；
∴V_{C′-A′B′C}：V_B′-A′BC：V_A′-ABC=

1

3

Sh：

2

3

Sh：

4

3

Sh=1：2：4．
故答案为：1：2：4．

点评：本题考查了求几何体体积的问题，解题时应灵活应用锥体体积公式，是中档题．