题目内容
已知α∈(0,
),求证:1<sinα+cosα<
.
| π |
| 2 |
| π |
| 2 |
考点:三角函数的最值
专题:三角函数的求值
分析:令y=sinα+cosα,则有 y2=1+sin2α,再根据α∈(0,
),根据正弦函数的定义域和值域求得y2的范围,即可证得不等式成立.
| π |
| 2 |
解答:
证明:令y=sinα+cosα,则有 y2=1+sin2α,再根据α∈(0,
),可得2α∈(0,π),
故y2∈(1,2],∴1<y≤
<
,即 1<sinα+cosα<
.
| π |
| 2 |
故y2∈(1,2],∴1<y≤
| 2 |
| π |
| 2 |
| π |
| 2 |
点评:本题主要考查正弦函数的定义域和值域,二倍角的正弦公式,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
已知集合A={x|1≤2x<8,x∈N*},则集合B={x-y|x∈A,y∈A}中元素的个数是( )
| A、1 | B、3 | C、5 | D、9 |
经过双曲线x2-y2=8的右焦点且斜率为2的直线被双曲线截得的线段的长是( )
A、
| ||||
B、7
| ||||
C、2
| ||||
D、
|
若函数f(x)=|ax|-x-a(a>0)有两个零点,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,+∞) | D、∅ |
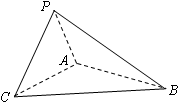 如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.
如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.