题目内容
已知△ABC的三个内角A，B，C的对边分别为a，b，c，且△ABC的面积为S=
accosB．
（1）若c=2a，求角A，B，C的大小；
（2）若a=2，且A=
，求△ABC的面积．
| ||
| 2 |
（1）若c=2a，求角A，B，C的大小；
（2）若a=2，且A=
| π |
| 3 |
考点：正弦定理,余弦定理
专题：解三角形
分析：（1）法一：根据正弦定理，建立条件关系，即可求出角A，B，C的大小；法二：根据余弦定理，建立条件关系，即可求出角A，B，C的大小．
（2）根据正弦定理求出c的大小，根据三角形的面积公式即可求△ABC的面积．
（2）根据正弦定理求出c的大小，根据三角形的面积公式即可求△ABC的面积．
解答：
解：由已知及三角形面积公式得S=
acsinB=
accosB，
化简得sinB=
cosB，
即tanB=
，又0＜B＜π，∴B=
．
（1）解法1：由c=2a，及正弦定理得，sinC=2sinA，
又∵A+C=
，
∴sin（
-A）=2sinA，
化简可得tanA=
，而0＜A＜
，
∴A=
，C=
．
解法2：由余弦定理得，b2=a2+c2-2accosB=a2+4a2-2a2=3a2，
∴b=
a，
∴a：b：c=1：
：2，知A=
，C=
．
（2）由A=
，B=
．可得△ABC为正三角形，又a=2，
∴S△ABC=
accosB=
．
| 1 |
| 2 |
| ||
| 2 |
化简得sinB=
| 3 |
即tanB=
| 3 |
| π |
| 3 |
（1）解法1：由c=2a，及正弦定理得，sinC=2sinA，
又∵A+C=
| 2π |
| 3 |
∴sin（
| 2π |
| 3 |
化简可得tanA=
| ||
| 3 |
| 2π |
| 3 |
∴A=
| π |
| 3 |
| π |
| 2 |
解法2：由余弦定理得，b2=a2+c2-2accosB=a2+4a2-2a2=3a2，
∴b=
| 3 |
∴a：b：c=1：
| 3 |
| π |
| 3 |
| π |
| 2 |
（2）由A=
| π |
| 3 |
| π |
| 3 |
∴S△ABC=
| ||
| 2 |
| 3 |
点评：本题主要考查正弦定理和余弦定理的应用，要求熟练掌握相应的定理以及三角形的面积公式．
练习册系列答案
相关题目
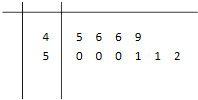一批食品，每袋的标准重量是50g，为了了解这批食品的实际重量情况，从中随机抽取10袋食品，称出各袋的重量（单位：g），并得到其茎叶图（如图）．
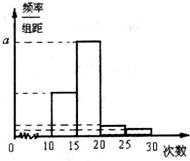对山东省实验中学高三年级学生参加社区服务次数进行统计，随机抽取m名学生作样本，得到这M名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表和频率分布直方图如图：