题目内容
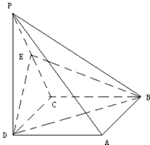 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.(Ⅰ)证明:PA∥平面EDB;
(Ⅱ)求三梭锥A一BDP的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:(I)根据中位线定理证明线线平行,再由线面平行的判定定理证明PA∥平面BDE;
(II)利用三棱锥的换底性,代入数据计算可得答案.
(II)利用三棱锥的换底性,代入数据计算可得答案.
解答:
解:(I)证明:连接AC交BD于O,连接OE,
∵ABCD是正方形,∴O为AC的中点,
又E是PC的中点,∴OE∥PA,
PA?平面BDE,OE?平面BDE,∴PA∥平面BDE;
(II)∵侧棱PD⊥底面ABCD,∴PD为三棱锥P-ABD的高,PD=DC=2,
∴VA-BDP=VP-ABD=
×S△ABD×PD=
×
×2×2×2=
.

∵ABCD是正方形,∴O为AC的中点,
又E是PC的中点,∴OE∥PA,
PA?平面BDE,OE?平面BDE,∴PA∥平面BDE;
(II)∵侧棱PD⊥底面ABCD,∴PD为三棱锥P-ABD的高,PD=DC=2,
∴VA-BDP=VP-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |

点评:本题考查了线面平行的证明及三棱锥的体积计算,利用线线平行证明线面平行是证明线面平行的基本方法.

练习册系列答案
相关题目

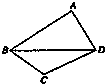 已知一颗粒子的等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在
已知一颗粒子的等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在