题目内容

17．已知0＜x＜y＜a＜1，设m=logax+logay，则m的取值范围为m＞2．

分析 先根据对数的运算性质化简，再由对数的单调性可得答案．

解答 解：因为0＜x＜y＜a＜1，
所以m=logax+logay=loga（xy）＞logaa2=2，
∴m＞2，
故答案为m＞2．

点评 本题主要考查对数的运算性质和对数函数的单调性．属基础题．

练习册系列答案
相关题目
4．公元前3世纪，古希腊欧几里得在《几何原本》里提出：“球的体积（V）与它的直径（d）的立方成正比”，此即V=kd3，与此类似，我们可以得到：
（1）正四面体（所有棱长都相等的四面体）的体积（V）与它的棱长（a）的立方成正比，即V=ma3；
（2）正方体的体积（V）与它的棱长（a）的立方成正比，即V=na3；
（3）正八面体（所有棱长都相等的八面体）的体积（V）与它的棱长（a）的立方成正比，即V=ta3；
那么m：n：t=（　　）
A．1：6$\sqrt{2}$：4B．$\sqrt{2}$：12：16C．$\frac{\sqrt{2}}{12}$：1：$\sqrt{2}$D．$\sqrt{2}$：6：4$\sqrt{2}$
5．已知直线x+y-5=0与两坐标轴围成的区域为M，不等式组$\left\{\begin{array}{l}y≤5-x\\ x≥0\\ y≥3x\end{array}\right.$所形成的区域为N，现在区域M中随机放置一点，则该点落在区域N的概率是（　　）
A．$\frac{3}{4}$B．$\frac{1}{2}$C．$\frac{1}{4}$D．$\frac{2}{3}$
5．函数f（x）=sinωx+$\sqrt{3}$cosωx+1的最小正周期为π，当x∈[m，n]时，f（x）至少有12个零点，则n-m的最小值为（　　）
A．12πB．$\frac{7π}{3}$C．6πD．$\frac{16π}{3}$
12．已知$\frac{sinα-cosα}{2sinα+3cosα}$=$\frac{1}{5}$，求tanα的值．
2．已知等差数列{bn}和各项都是正数的数列{an}，且a1=b1=1，b2+b4=10，满足an2-2anan+1+an-2an+1=0
（1）求{an}和{bn}通项公式；
（2）设cn=$\frac{1}{a_n}+{b_n}$，求数列{cn}的前n项和．
9．设$f（x）=\left\{\begin{array}{l}2{e^{x-1}}，x＜2\\{log_3}（{x^2}-1），x≥2\end{array}\right.$则f（f（1））=1，不等式f（x）＞2的解集为$（1，2）∪（\sqrt{10}，+∞）$．
6．我们把三个集合中，通过两次连线后能够有关系的两个数字的关系称为”鼠标关系”，如图1，可称a与q，b与q，c与q都为”鼠标关系”集合A={a，b，c，d}，通过集合 B={1，2，3} 与集合C={m，n}最多能够产生24条”鼠标关系”，（只要有一条连线不同则”鼠标关系”不同）
7．一个几何体的三视图如图所示，则此几何体的体积为（　　）
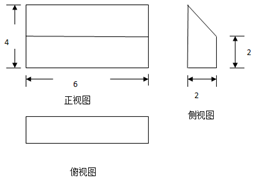
A．16B．36C．48D．72

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网