题目内容
9.设$f(x)=\left\{\begin{array}{l}2{e^{x-1}},x<2\\{log_3}({x^2}-1),x≥2\end{array}\right.$则f(f(1))=1,不等式f(x)>2的解集为$(1,2)∪(\sqrt{10},+∞)$.分析 根据函数的解析式求出f(1)的值是2,从而求出f(2)的值即可;不等式f(x)>2即2ex-1>2或log3(x2-1)>2,即ex-1>1=e0,或x2-1>9,解出即可.
解答 解:$f(x)=\left\{\begin{array}{l}2{e^{x-1}},x<2\\{log_3}({x^2}-1),x≥2\end{array}\right.$,
f(1)=2•e1-1=2,
故f(f(1))=f(2)=log3(4-1)=1,
若f(x)>2,
则2ex-1>2(x<2)或log3(x2-1)>2(x≥2),
即ex-1>1=e0,或x2-1>9,
解得:1<x<2或x>$\sqrt{10}$,
故答案为:1,$(1,2)∪(\sqrt{10},+∞)$
点评 本题考查了解指数、对数不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
1.已知点A是抛物线M:y2=2px(p>0)与圆$C:{x^2}+{(y-2\sqrt{2})^2}={a^2}$在第一象限的公共点,且点A到抛物线M焦点F的距离等于a.若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a,则p为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
18. 已知一个几何体的三视图如右图所示(单位:cm),则该几何体的体积为( )
已知一个几何体的三视图如右图所示(单位:cm),则该几何体的体积为( )
 已知一个几何体的三视图如右图所示(单位:cm),则该几何体的体积为( )
已知一个几何体的三视图如右图所示(单位:cm),则该几何体的体积为( )| A. | 12cm3 | B. | 16cm3 | C. | 18cm3 | D. | 20cm3 |
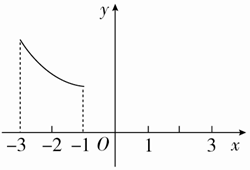 定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.
定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.