题目内容
若函数y=f(x)是函数y=ax2(a>0且a≠1)的反函数,其图象经过点(
,a),则f(x)( )
| a |
| A、log2x | ||
B、log
| ||
C、
| ||
| D、x2 |
考点:反函数
专题:函数的性质及应用
分析:利用互为反函数的定义域与值域互换的性质即可得出.
解答:
解:∵函数y=f(x)是函数y=ax2(a>0且a≠1)的反函数,其图象经过点(
,a),
∴
=a×a2,解得a=1.
∴f(x)=x2.
故选:D.
| a |
∴
| a |
∴f(x)=x2.
故选:D.
点评:本题考查了互为反函数的定义域与值域互换的性质,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
下列命题中正确的是( )
A、若
| ||||||||||||
B、若
| ||||||||||||
C、若
| ||||||||||||
D、若
|
在下面的程序框图中,若输入的a,b,c分别为9,-10,0,则输出的a的值为( )


| A、0 | B、9 |
| C、-10 | D、以上均不是 |
在用数学归纳法证明等式1+2+3+…+2n=n(2n+1)时,当n=1时的左边等于( )
| A、1 | B、2 | C、3 | D、4 |
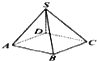 如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为( )
如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为( )| A、60 | B、480 |
| C、420 | D、70 |
两位运动员投篮,投中的概率分别为0.6和0.7,每人各投2次,投中次数相等的概率为( )
| A、0.248 4 |
| B、0.25 |
| C、0.9 |
| D、0.392 4 |
函数f (x)=|2x-a|+1 的定义域为[p,q],值域为[1,2],则q-p的最大值为( )
| A、1 | B、2 |
| C、a+1 | D、2 a |
已知数列{an}满足a1>0,且an+1=
an,则数列{an}是( )
| 1 |
| 2 |
| A、递增数列 | B、递减数列 |
| C、常数列 | D、摆动数列 |