题目内容
正三棱锥P-ABC侧棱长为
，侧棱与底面ABC所成的角为60°，则该正三棱锥外接球半径为 ．
| 3 |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：过点P作PH⊥平面ABC于H，可得∠PAH是直线PA与底面ABC所成的角，得∠PAH=60°．由PA=PB=PC，得外接球心O必定在PH上，连接OA，可得△POA是底角等于30°的等腰三角形，从而得到外接球的半径R=OA=1．
解答：
解：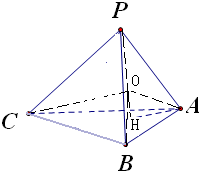
过点P作PH⊥平面ABC于H，则
∵AH是PA在平面ABC内的射影
∴∠PAH是直线PA与底面ABC所成的角，得∠PAH=60°，
∴Rt△PAH中，AH=PAcos60°=
，PH=PAsin60°=
设三棱锥外接球的球心为O，
∵PA=PB=PC，∴P在平面ABC内的射影H是△ABC的外心
由此可得，外接球心O必定在PH上，连接OA、OB、OC
∵△POA中，OP=OA，
∴∠OAP=∠OPA=30°，可得PA=
OA=
，
∴三棱锥外接球的半径R=OA=1
故答案为：1．
过点P作PH⊥平面ABC于H，则∵AH是PA在平面ABC内的射影
∴∠PAH是直线PA与底面ABC所成的角，得∠PAH=60°，
∴Rt△PAH中，AH=PAcos60°=
| ||
| 2 |
| 3 |
| 2 |
设三棱锥外接球的球心为O，
∵PA=PB=PC，∴P在平面ABC内的射影H是△ABC的外心
由此可得，外接球心O必定在PH上，连接OA、OB、OC
∵△POA中，OP=OA，
∴∠OAP=∠OPA=30°，可得PA=
| 3 |
| 3 |
∴三棱锥外接球的半径R=OA=1
故答案为：1．
点评：本题给出三棱锥的三条侧棱两两相等，在已知一条侧棱与底面所成角的情况下求外接球的体积，着重考查了直线与平面所成角的定义、球内接多面体和球体积的求法等知识，属于中档题．
练习册系列答案
相关题目
若函数y=f（x）是函数y=ax2（a＞0且a≠1）的反函数，其图象经过点（
，a），则f（x）（ ）
| a |
| A、log2x | ||
B、log
| ||
C、
| ||
| D、x2 |