题目内容
在平行四边形ABCD中，A（1，1），
=（6，0），点M是线段AB的中点，线段CM与BD交于点P（x，y）．当|
|=|
|时，求x，y满足的方程．
| AB |
| AB |
| AD |
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：如图所示，由于平行四边形ABCD中，A（1，1），
=（6，0），可得
=
+（6，0），点M是线段AB的中点，DC∥AB，可得
=
=
，因此
=2
，可得
=（3x-15，3y-3）．利用|
|=|
|，即可得出．
| AB |
| OB |
| OA |
| DP |
| PB |
| DC |
| MB |
| 2 |
| 1 |
| DP |
| PB |
| AD |
| AB |
| AD |
解答：
解：如图所示，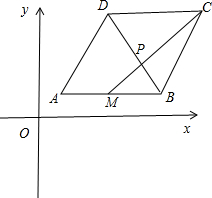
∵平行四边形ABCD中，A（1，1），
=（6，0），
∴
=
+（6，0）=（7，1），
∵点M是线段AB的中点．
又∵DC∥AB，
∴
=
=
，
∴
=2
，
∴
=
-2
=（x，y）-2（7-x，1-y）=（3x-14，3y-2）．
∴
=（3x-15，3y-3）．
∵|
|=|
|，
∴
=6．
化为（x-5）2+（y-1）2=4，（x≠3，7）．
∵平行四边形ABCD中，A（1，1），
| AB |
∴
| OB |
| OA |
∵点M是线段AB的中点．
又∵DC∥AB，
∴
| DP |
| PB |
| DC |
| MB |
| 2 |
| 1 |
∴
| DP |
| PB |
∴
| OD |
| OP |
| PB |
∴
| AD |
∵|
| AB |
| AD |
∴
| (3x-15)2+(3y-3)2 |
化为（x-5）2+（y-1）2=4，（x≠3，7）．
点评：本题查克拉平行四边形的性质、向量的坐标运算、向量模的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数f(x)=
的定义域为（ ）
| 1 |
| log3(3x-2) |
A、[
| ||
B、（
| ||
C、[
| ||
D、（
|
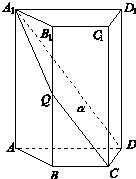如图，四棱柱ABCD A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD=2BC．过A1，C，D三点的平面记为α，BB1与α的交点为Q．
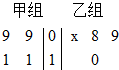以下茎叶图记录了甲、乙两组各四名同学的植树棵树． 乙组记录中有一个数据模糊，无法辨认，在图中以X表示．