题目内容
若函数f(x)=x2+mx-2在(-∞,2]是单调减函数,在[2,+∞)是单调增函数,则实数m= .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据二次函数的性质,得到x=-
=2,解出即可.
| m |
| 2 |
解答:
解:由题意得:
对称轴x=-
=2,
解得:m=-4,
故答案为:-4.
对称轴x=-
| m |
| 2 |
解得:m=-4,
故答案为:-4.
点评:本题考查了二次函数的性质,考查了函数的单调性,是一道基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
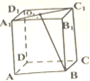 如图,在长方体ABCD-A1B1C1D1中,A1C1的中点为O1,AB=BC=2,AA1=3,求异面直线BO1与A1D1所成角的余弦值.
如图,在长方体ABCD-A1B1C1D1中,A1C1的中点为O1,AB=BC=2,AA1=3,求异面直线BO1与A1D1所成角的余弦值. 连线方式表示为
连线方式表示为