题目内容
7.2015年高中生技能大赛中三所学校分别有3名、2名、1名学生获奖,这6名学生要排成一排合影,则同校学生排在一起的概率是( )| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{5}$ |
分析 把第一个及第二个学校的学生看做整体,求出同校学生排在一起的方法数,再求出三个学校的学生随便排有多少种方法,由古典概型的概率计算公式得所求概率.
解答 解:由已知把第一个及第二个学校的学生看做整体得同校学生排在一起共$A_3^3A_2^2A_3^3$种方法,
而三个学校的学生随便排有$A_6^6$种方法,
由古典概型的概率计算公式得所求概率:
$P=\frac{A_3^3A_2^2A_3^3}{A_6^6}=\frac{12}{6×5×4}=\frac{1}{10}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
17.已知函数f(x)=|2x-1|,g(x)=x2-(2+3k)x+2k+1,若函数y=g[f(x)]有3个不同零点,则k的范围是( )
| A. | k=-$\frac{1}{2}$或k>0 | B. | -$\frac{1}{2}$<k<0或k>0 | C. | k≥-$\frac{1}{2}$ | D. | k≥0 |
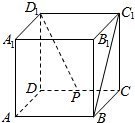 如图,在正方体ABCD-A1B1C1D1中,P为棱DC的中点,则D1P与BC1所在的直线所成角的余弦值等于$\frac{\sqrt{10}}{5}$.
如图,在正方体ABCD-A1B1C1D1中,P为棱DC的中点,则D1P与BC1所在的直线所成角的余弦值等于$\frac{\sqrt{10}}{5}$.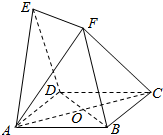 如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC.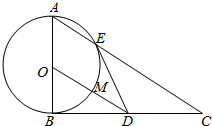 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.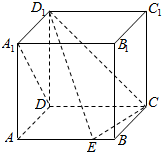 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.