题目内容

17．设函数f（x）=ex+a+x，g（x）=ln（x+3）-4e-x-a，其中e为自然对数的底数，若存在实数x0，使得f（x0）-g（x0）=2成立，则实数a值为（　　）
A．-2+ln2B．1+ln2C．-1-ln2D．2+ln2

分析 令f（x）-g（x）=x+ex+a-1n（x+3）+4e-a-x，运用导数求出y=x-ln（x+3）的最小值；运用基本不等式可得ex+a+4e-a-x≥4，从而可证明f（x）-g（x）≥2，由等号成立的条件，从而解得a．

解答 解：令f（x）-g（x）=x+ex+a-1n（x+3）+4e-a-x，
令y=x-ln（x+3），y′=1-$\frac{1}{x+3}$=$\frac{x+2}{x+3}$，
故y=x-ln（x+3）在（-3，-2）上是减函数，（-2，+∞）上是增函数，
故当x=-2时，y有最小值-2-0=-2，
而ex+a+4e-a-x≥4（当且仅当ex+a=4e-a-x，即x=-a+ln2时，等号成立）；
故f（x）-g（x）≥2（当且仅当等号同时成立时，等号成立）；
故x=-a+ln2=-2，
即a=2+ln2．
故选：D．

点评 本题考查了导数的综合应用及基本不等式的应用，同时考查了方程的根与函数的零点的关系应用，属于中档题．

练习册系列答案
相关题目
7．已知函数f（x）=lnx，若4f′（x）+x≥a恒成立，则a的取值范围是（　　）
A．a≥4B．a≤4C．a≥2$\sqrt{2}$D．a≤2$\sqrt{2}$
8．已知函数g（x）的导函数g'（x）=ex，且g（0）g'（1）=e，（其中e为自然对数的底数）．若?x∈（0，+∞），使得不等式$g（x）＜\frac{x-m+3}{{\sqrt{x}}}$成立，则实数m的取值范围是（　　）
A．（-∞，1）B．（-∞，3）C．（3，+∞）D．（-∞，4-e）
5．等差数列{an}的前n项和是Sn，且a3=1，a5=4，则S13=（　　）
A．39B．91C．48D．51
12．设两个非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）=0，且2|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=（　　）
A．2$\sqrt{3}$B．2C．4D．8
2．已知离心率为$\frac{1}{2}$的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点M（2，0），过点Q（1，0）的直线与椭圆C相交于A，B两点，设点P（4，3），记PA，PB的斜率分别为k1，k2
（Ⅰ）求椭圆C的方程；
（Ⅱ）探讨k1+k2是否为定值？如果是，求出该定值，如果不是，求出k1+k2的取值范围．
9．三棱锥P-ABC中，PC⊥平面ABC，∠CAB=90°，PC=3，AC=4，AB=5，则此三棱锥外接球的表面积为50π．
6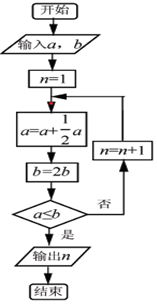．执行如图所示的程序框图，若输入的a=16，b=4，则输出的n=（　　）
A．4B．5C．6D．7
7．已知{an}为等差数列，Sn为其前n项和，若a1=2，S3=15，则a6=（　　）
A．17B．14C．13D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网