题目内容
8.已知函数g(x)的导函数g'(x)=ex,且g(0)g'(1)=e,(其中e为自然对数的底数).若?x∈(0,+∞),使得不等式$g(x)<\frac{x-m+3}{{\sqrt{x}}}$成立,则实数m的取值范围是( )| A. | (-∞,1) | B. | (-∞,3) | C. | (3,+∞) | D. | (-∞,4-e) |
分析 由g'(x)=ex,可设g(x)=ex+c,再由g(0)g'(1)=e可得g(x)<$\frac{x-m+3}{\sqrt{x}}$成立,分离出参数m后可得m<x-ex$\sqrt{x}$+3,令h(x)=x-ex$\sqrt{x}$+3,则问题可转化为:m<h(x)max,利用导数可求得h(x)max.
解答 解:∵函数g(x)的导函数g'(x)=ex,
∴g(x)=ex+c,
又∵g(0)g'(1)=e,
∴(1+c)e=e⇒c=0,∴g(x)=ex,
∵?x∈(0,+∞),使得不等式g(x)<$\frac{x-m+3}{\sqrt{x}}$成立,
∴?x∈(0,+∞),使得m<x-ex$\sqrt{x}$+3成立,
令h(x)=x-ex$\sqrt{x}$+3,则问题可转化为:m<h(x)max,
对于h(x)=x-ex$\sqrt{x}$+3,x∈(0,+∞),
由于h′(x)=1-ex($\sqrt{x}$+$\frac{1}{2\sqrt{x}}$),
当x∈(0,+∞)时,
∵ex>1,$\sqrt{x}$+$\frac{1}{2\sqrt{x}}$≥2 $\sqrt{\sqrt{x}•\frac{1}{2\sqrt{x}}}$=$\sqrt{2}$,
∴ex($\sqrt{x}$+$\frac{1}{2\sqrt{x}}$)>1,
∴h'(x)<0,从而h(x)在(0,+∞)上为减函数,
∴h(x)<h(0)=3,∴m<3;
故选:B.
点评 本题考查利用导数研究函数的极值、最值及证明不等式等问题,考查恒成立问题,考查转化思想,考查学生的推理论证能力、分析解决问题的能力,本题综合性强,能力要求较高.

练习册系列答案
相关题目
16.已知sin(α$-\frac{π}{8}$)=$\frac{4}{5}$,则cos(α+$\frac{3π}{8}$)=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
3.数列{an}满足:a1=-9,an+1-an=2,Sn是其前n项和,则S10=( )
| A. | 0 | B. | -9 | C. | 10 | D. | -10 |
17.设函数f(x)=ex+a+x,g(x)=ln(x+3)-4e-x-a,其中e为自然对数的底数,若存在实数x0,使得f(x0)-g(x0)=2成立,则实数a值为( )
| A. | -2+ln2 | B. | 1+ln2 | C. | -1-ln2 | D. | 2+ln2 |
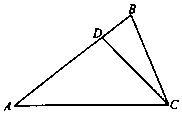 如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.
如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.