题目内容
等差数列{an}的公差为d,前n项和为Tn,设Cn=an2-an+12
(1)判断数列{Cn}是否为等差数列并说明理由;
(2)若a1+a3+a5+…a25=130,a2+a4+a6+…+a26=143-13k(k是常数),试写出数列{Cn}的通项公式;
(3)在(2)的条件下,若数列{Cn}的前n项和Sn,问是否存在实数k,使得Sn当且仅当n=12时取得最大值?若存在,求出k的取值范围;若不存在,请说明理由.
(1)判断数列{Cn}是否为等差数列并说明理由;
(2)若a1+a3+a5+…a25=130,a2+a4+a6+…+a26=143-13k(k是常数),试写出数列{Cn}的通项公式;
(3)在(2)的条件下,若数列{Cn}的前n项和Sn,问是否存在实数k,使得Sn当且仅当n=12时取得最大值?若存在,求出k的取值范围;若不存在,请说明理由.
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:(1)设{an}的公差为d,则cn+1-cn=(an+12-an+22)-(an2-an+12)=-2d2,所以数列{cn}是以-2d2为公差的等差数列;
(2)由a1+a3+…+a25=130a2+a4+…+a26=143-13k,知13d=13-13k,d=1-k,由此能导出an=a1+(n-1)d=(1-kn+(13k-3)),由此能求出数列{cn}的通项公式;
(3)因为当且仅当n=12时Sn最大,所以c12>0,c13<0,由此能求出k的取值范围.
(2)由a1+a3+…+a25=130a2+a4+…+a26=143-13k,知13d=13-13k,d=1-k,由此能导出an=a1+(n-1)d=(1-kn+(13k-3)),由此能求出数列{cn}的通项公式;
(3)因为当且仅当n=12时Sn最大,所以c12>0,c13<0,由此能求出k的取值范围.
解答:
解:(1)设{an}的公差为d,则cn+1-cn=(an+12-an+22)-(an2-an+12)
=2an+12-(an+1-d)2-(an+1+d)2=-2d2
∴数列{cn}是以-2d2为公差的等差数列;
(2)∵a1+a3+…+a25=130a2+a4+…+a26=143-13k
∴两式相减:13d=13-13k,
∴d=1-k,
∴13a1+
×2d=130,
∴a1=-2+12k,
∴an=a1+(n-1)d=(1-k)n+(13k-3),
∴cn=an2-an+12=(an+an+1)(an-an+1)
=26k2-32+6-(2n+1)(1-k2)
=-2(1-k)2•n+25k2-30k+5;
(3)因为当且仅当n=12时Sn最大,
∴有c12>0,c13<0,
即
,
解得
,即有k>21或k<-19.
故存在实数k,使得Sn当且仅当n=12时取得最大值,
k的取值范围是:k>21或k<-19.
=2an+12-(an+1-d)2-(an+1+d)2=-2d2
∴数列{cn}是以-2d2为公差的等差数列;
(2)∵a1+a3+…+a25=130a2+a4+…+a26=143-13k
∴两式相减:13d=13-13k,
∴d=1-k,
∴13a1+
| 13×12 |
| 2 |
∴a1=-2+12k,
∴an=a1+(n-1)d=(1-k)n+(13k-3),
∴cn=an2-an+12=(an+an+1)(an-an+1)
=26k2-32+6-(2n+1)(1-k2)
=-2(1-k)2•n+25k2-30k+5;
(3)因为当且仅当n=12时Sn最大,
∴有c12>0,c13<0,
即
|
解得
|
故存在实数k,使得Sn当且仅当n=12时取得最大值,
k的取值范围是:k>21或k<-19.
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用.

练习册系列答案
相关题目
若实数x,y满足约束条件
,则z=x+y的最大值是4,则a=( )
|
| A、2 | B、3 | C、3或1 | D、4 |
已知函数f(x)=
对任意x1,x2∈R(x1≠x2),恒有(x1-x2)[f(x1)-f(x2)]>0
,则实数a的取值范围为( )
|
,则实数a的取值范围为( )
| A、(1,+∞) |
| B、[4,8) |
| C、(4,8) |
| D、(1,8) |
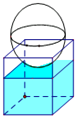 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为