题目内容
18.在△ABC中,A=30°,AB=3,$AC=2\sqrt{3}$,且$\overrightarrow{AD}+2\overrightarrow{BD}=\overrightarrow 0$,则$\overrightarrow{AC}.\overrightarrow{CD}$=-6.分析 根据题意建立直角平面坐标系,得出△ABC是直角三角形,利用坐标表示向量$\overrightarrow{AC}$、$\overrightarrow{CD}$,求出$\overrightarrow{AC}$•$\overrightarrow{CD}$即可.
解答 解:如图所示,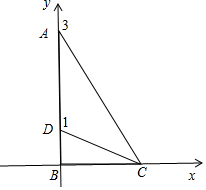
△ABC中,A=30°,AB=3,$AC=2\sqrt{3}$,
∴cos30°=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠ABC=90°,
∴BC=$\frac{1}{2}$AC=$\sqrt{3}$;
又$\overrightarrow{AD}+2\overrightarrow{BD}=\overrightarrow 0$,
∴A(0,3),D(0,1),C($\sqrt{3}$,0);
∴$\overrightarrow{AC}$=($\sqrt{3}$,-3),$\overrightarrow{CD}$=(-$\sqrt{3}$,1),
∴$\overrightarrow{AC}$•$\overrightarrow{CD}$=$\sqrt{3}$×(-$\sqrt{3}$)-3×1=-6.
故答案为:-6.
点评 本题考查了平面向量的数量积运算问题,是基础题.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
8.一个三棱锥的三视图如下图所示,则该几何体的体积为( )
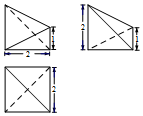

| A. | 1 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{8\sqrt{3}}{3}$ |
9.设z=-1+3i,则z的共轭复数为( )
| A. | -1+3i | B. | -1-3i | C. | 1+3i | D. | 1-3i |
3.如图所示的程序框图,运行后输出的结果为( )


| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
8.函数y=|x-4|+|x-6|的最小值为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 4 | D. | 6 |