题目内容
8．函数y=|x-4|+|x-6|的最小值为（ ）| A． | 2 | B． | $\sqrt{2}$ | C． | 4 | D． | 6 |
分析 由函数表达式，去掉绝对值，把函数写成分段函数的形式，再画出函数的图象，得函数的最小值即可．
解答 
解：数形结合法：y=|x-4|+|x-6|=$\left\{\begin{array}{l}{10-2x，x≤4}\\{2，4＜x＜6}\\{2x-10，x≥6}\end{array}\right.$，
画出它的图象，如图，由图知，
y≥2，
故选：A．
点评 本题主要考查了带绝对值的函数，体现数形结合和分类讨论的数学思想方法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．
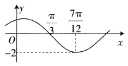已知函数f（x）=Asin（wx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=Asin（wx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=2sin（2x-$\frac{π}{3}$） | B． | g（x）=2sin（2x+$\frac{π}{6}$） | C． | g（x）=-2sin（2x-$\frac{π}{3}$） | D． | g（x）=-2sin（2x+$\frac{π}{6}$） |
16．
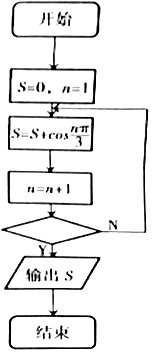执行如图所示的程序框图，若输出S的值为-1，则判断框内，对于下列四个关于n的条件的选项，不能填入的是（ ）
执行如图所示的程序框图，若输出S的值为-1，则判断框内，对于下列四个关于n的条件的选项，不能填入的是（ ）| A． | n＞3？ | B． | n＞5？ | C． | n＞32？ | D． | n＞203？ |
3．甲、乙、丙三位同学被问到是否去过济南、潍坊、青岛三个城市时，甲说：我去过的城市比乙多，但没去过潍坊；乙说：我没去过青岛；丙说：我们三人去过同一城市；由此可判断乙去过的城市为（ ）
| A． | 济南 | B． | 青岛 | C． | 济南和潍坊 | D． | 济南和青岛 |
13．实部为-2，虚部为1的复数所对应的点位于复平面的（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
20．在三角形ABC中，$\overrightarrow{BC}=\overrightarrow{a}，\overrightarrow{CA}=\overrightarrow{b}$，则$\overrightarrow{AB}$=（ ）
| A． | $\overrightarrow a-\overrightarrow b$ | B． | $\overrightarrow b-\overrightarrow a$ | C． | $\overrightarrow b+\overrightarrow a$ | D． | $-\overrightarrow a-\overrightarrow b$ |
17．
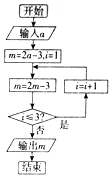《九章算术》是中国古代数学名著，体现了古代劳动人民数学的智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出的m的值为35，则输入的a的值为（ ）
《九章算术》是中国古代数学名著，体现了古代劳动人民数学的智慧，其中第六章“均输”中，有一竹节容量问题，某教师根据这一问题的思想设计了如图所示的程序框图，若输出的m的值为35，则输入的a的值为（ ）| A． | 4 | B． | 5 | C． | 7 | D． | 11 |
18．若函数f（x）=（x2+x-2）（x2+ax+b）是偶函数，则f（x）的最小值为（ ）
| A． | $\frac{9}{4}$ | B． | $\frac{11}{4}$ | C． | -$\frac{9}{4}$ | D． | -$\frac{11}{4}$ |