题目内容
8．一个三棱锥的三视图如下图所示，则该几何体的体积为（ ）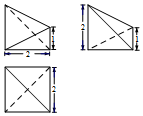
| A． | 1 | B． | $\frac{4\sqrt{3}}{3}$ | C． | 2 | D． | $\frac{8\sqrt{3}}{3}$ |
分析 由三视图可得到如图所示几何体，该几何体是由正方体切割得到的，三棱锥的高为$\sqrt{3}$，可得几何体的体积．
解答 
解：由三视图可得到如图所示几何体，该几何体是由正方体切割得到的，三棱锥的高为$\sqrt{3}$，
∴该几何体的体积为$\frac{1}{3}×\frac{\sqrt{3}}{4}×（2\sqrt{2}）^{2}×\sqrt{3}$=2．
故选C．
点评 本题考查几何体的体积，考查空间想象能力，计算能力，是基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
18．阅读下面的程序框图，运行相应的程序，输出的结果为（ ）
| A． | -3 | B． | -$\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | 2 |
19．对于R上可导的任意函数f（x），若满足（x-1）f′（x）≤0，则必有（ ）
| A． | f（0）+f（2）＜2f（1） | B． | f（0）+f（2）≤2f（1） | C． | f（0）+f（2）≥2f（1） | D． | f（0）+f（2）＞2f（1） |
16．若某程序框图如图所示，则输出的p的值是（ ）
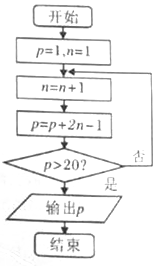
| A． | 49 | B． | 36 | C． | 25 | D． | 16 |
3．
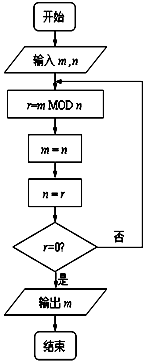如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“mMOD n”表示m除以n的余数），若输入的m，n分别为72，15，则输出的m=（ ）
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“mMOD n”表示m除以n的余数），若输入的m，n分别为72，15，则输出的m=（ ）| A． | 12 | B． | 3 | C． | 15 | D． | 45 |
13．“p∨q为假命题”是“￢p为真命题”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
20．函数f（x）=ln（-x2+2x+3）的定义域为（ ）
| A． | {x|-3＜x＜1} | B． | {x|-1＜x＜3}． | C． | {x|x＜-3或x＞1} | D． | {x|x＜-1或x＞3} |