题目内容
9．设z=-1+3i，则z的共轭复数为（ ）| A． | -1+3i | B． | -1-3i | C． | 1+3i | D． | 1-3i |
分析 直接利用共轭复数的概念得答案．
解答 解：∵z=-1+3i，
∴z的共轭复数$\overline{z}=-1-3i$，
故选：B．
点评 本题考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
19．对于R上可导的任意函数f（x），若满足（x-1）f′（x）≤0，则必有（ ）
| A． | f（0）+f（2）＜2f（1） | B． | f（0）+f（2）≤2f（1） | C． | f（0）+f（2）≥2f（1） | D． | f（0）+f（2）＞2f（1） |
20．函数f（x）=ln（-x2+2x+3）的定义域为（ ）
| A． | {x|-3＜x＜1} | B． | {x|-1＜x＜3}． | C． | {x|x＜-3或x＞1} | D． | {x|x＜-1或x＞3} |
4．执行如图所示的程序框图，输出S值为（ ）
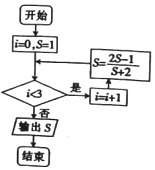
| A． | $-\frac{31}{15}$ | B． | $-\frac{7}{5}$ | C． | $-\frac{31}{17}$ | D． | $-\frac{9}{13}$ |
14．
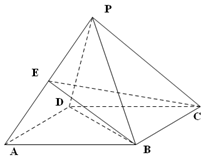如图，四棱锥P-ABCD的底面ABCD是边长为2的菱形，∠BAD=60°，PB=PD=2，PA=$\sqrt{6}$，E为PA的中点，
（1）证明：PC∥面EBD；
（2）求三棱锥P-BCE的体积．
如图，四棱锥P-ABCD的底面ABCD是边长为2的菱形，∠BAD=60°，PB=PD=2，PA=$\sqrt{6}$，E为PA的中点，（1）证明：PC∥面EBD；
（2）求三棱锥P-BCE的体积．
19．
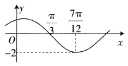已知函数f（x）=Asin（wx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（ ）
已知函数f（x）=Asin（wx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=2sin（2x-$\frac{π}{3}$） | B． | g（x）=2sin（2x+$\frac{π}{6}$） | C． | g（x）=-2sin（2x-$\frac{π}{3}$） | D． | g（x）=-2sin（2x+$\frac{π}{6}$） |