题目内容
6.下列是我国2010年至2016年生活垃圾无害化处理量(单位:亿吨)的折线图.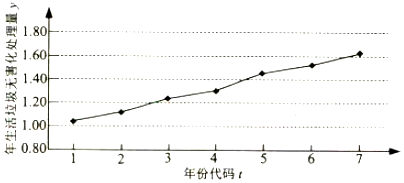
(1)由折线图看出,可用线性回归模型拟合y与t的关系,求y关于t的回归方程(系数精确到0.01);
(2)预测2018年我国生活垃圾无害化处理量.
附注:参考数据:$\sum_{i=1}^{7}$yi=9.32,$\sum_{i=1}^{7}$tiyi=40.17
回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$t中斜率和截距的最小二乘法估计公式分别为:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.
分析 (1)求出$\widehat{b}$,$\widehat{a}$的值,代入回归方程即可;(2)将t=9代入回归方程即可.
解答 解:(1)由折线图中数据和附注中参考数据得:
$\overline t=4$,$\sum_{i=1}^7{t_i^2-7{{\overline t}^2}=28}$,$\sum_{i=1}^7{{t_i}{y_i}-7\overline t\overline y}=\sum_{i=1}^7{{t_i}{y_i}-\overline t\sum_{i=1}^7{y_i}}=40.17-4×9.32=2.89$,
由$\overline y=\frac{9.32}{7}≈1.331$及(1)得$\widehat{b}$=$\frac{2.89}{28}$≈0.103,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$≈1.331-0.103×4≈0.92,
所以,y关于t的回归方程为:$\widehat{y}$=0.92+0.10t;
(2)将2018年对应的t=9代入回归方程得:
$\widehat{y}$=0.92+0.10×9=1.82,
所以预测2018年我国生活垃圾无害化处理量将约为1.82亿吨.
点评 本题考查的知识点是线性回归方程,回归分析,计算量比较大,计算时要细心.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
16.若某程序框图如图所示,则输出的p的值是( )
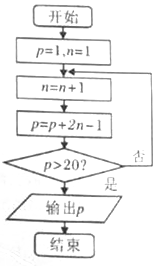

| A. | 49 | B. | 36 | C. | 25 | D. | 16 |
14.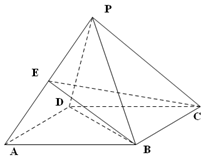 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,
(1)证明:PC∥面EBD;
(2)求三棱锥P-BCE的体积.
 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,(1)证明:PC∥面EBD;
(2)求三棱锥P-BCE的体积.
16.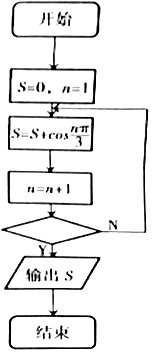 执行如图所示的程序框图,若输出S的值为-1,则判断框内,对于下列四个关于n的条件的选项,不能填入的是( )
执行如图所示的程序框图,若输出S的值为-1,则判断框内,对于下列四个关于n的条件的选项,不能填入的是( )
 执行如图所示的程序框图,若输出S的值为-1,则判断框内,对于下列四个关于n的条件的选项,不能填入的是( )
执行如图所示的程序框图,若输出S的值为-1,则判断框内,对于下列四个关于n的条件的选项,不能填入的是( )| A. | n>3? | B. | n>5? | C. | n>32? | D. | n>203? |