题目内容
设m,n是两条不同的直线,α、β、γ是三个不同的平面,给出下列命题,正确的是( )
| A、若m?β,α⊥β,则m⊥α |
| B、若m∥α,m⊥β,则α⊥β |
| C、若α⊥β,α⊥γ,则β⊥γ |
| D、若α∩γ=m,β∩γ=n,m∥n,则α∥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据线面平行的性质定理,线面垂直的第二判定定理,面面垂直的判定定理,可判断B中结论正确,而由空间点线面关系的几何特征,可判断其它结论均不一定成立.
解答:
解:若m?β,α⊥β,则m与α的关系不确定,故A错误;
若m∥α,则存在直线n?α,使m∥n,又由m⊥β,可得n⊥β,进而由面面垂直的判定定理得到α⊥β,故B正确;
若α⊥β,α⊥γ,则β与γ关系不确定,故C错误;
若α∩γ=m,β∩γ=n,m∥n,则α与β可能平行,也可能相交(此时交线与m,n均平行),故D错误;
故选:B
若m∥α,则存在直线n?α,使m∥n,又由m⊥β,可得n⊥β,进而由面面垂直的判定定理得到α⊥β,故B正确;
若α⊥β,α⊥γ,则β与γ关系不确定,故C错误;
若α∩γ=m,β∩γ=n,m∥n,则α与β可能平行,也可能相交(此时交线与m,n均平行),故D错误;
故选:B
点评:本题考查平面的基本性质和推论,是基础题,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
设常数a>0,(ax2+
)4的展开式中x3的系数为
,则a=( )
| 1 | ||
|
| 3 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、1 |
函数f(x)=x3-3bx+3b在(0,1)内有极小值的充分不必要条件是( )
| A、b∈(0,1) | ||
| B、b∈(1,+∞) | ||
C、b∈(
| ||
| D、b∈(-∞,1) |
曲线y=sinx,x∈[0,2π]与坐标轴围成的面积( )
| A、4 | B、3 | C、2 | D、0 |
以F(-3,0)为焦点的抛物线的标准方程为( )
| A、y2=6x |
| B、y2=-6x |
| C、y2=12x |
| D、y2=-12x |
已知a>0,b>0且a+2b=2,若
+
>m恒成立,则实数m的取值范围为( )
| 2 |
| a |
| 1 |
| b |
| A、(-∞,8) |
| B、(8,+∞) |
| C、(-∞,4) |
| D、(4,+∞) |
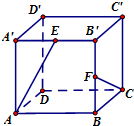 正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为
正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为