题目内容
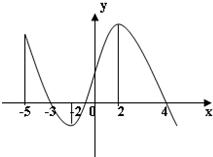 如图所示是f′(x)的图象,则正确的判断个数是( )
如图所示是f′(x)的图象,则正确的判断个数是( )(1)f(x)在(-5,-3)上是减函数;
(2)x=4是极大值点;
(3)x=2是极值点;
(4)f(x)在(-2,2)上先减后增.
| A、0 | B、1 | C、2 | D、3 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:计算题,导数的概念及应用
分析:根据导函数看正负,原函数看增减,函数在极值点处导数符号改变,即可得到结论.
解答:
解:根据导函数看正负,原函数看增减,可得f(x)在(-5,-3)上是增函数;在x=4的左右附近,导数值先正后负,可得函数先增后减,从而可知在x=4处函数取得极大值;f(x)在(-2,2)上先减后增,x=2的左右附近导数为正,故不是极值点.
故选:C.
故选:C.
点评:本题考查导函数的图象,考查函数的单调性与极值,解题的关键是利用导函数看正负,原函数看增减,函数在极值点处导数符号改变.

练习册系列答案
相关题目
用“更相减损术”求98和63的最大公约数,要做减法的次数是( )
| A、3次 | B、4次 | C、5次 | D、6次 |
函数f(x)=x3-3bx+3b在(0,1)内有极小值的充分不必要条件是( )
| A、b∈(0,1) | ||
| B、b∈(1,+∞) | ||
C、b∈(
| ||
| D、b∈(-∞,1) |
已知定义在R上的奇函数f(x)满足f(x+2)=-f(x-2),且在区间[0,2]上是减函数.若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=( )
| A、-8 | B、8 | C、4 | D、-4 |
执行如图所示的框图,如果输入的x∈[0,
],则输出的y值属于( )

| π |
| 2 |

| A、[0,1] | ||||
B、[0,
| ||||
C、[
| ||||
D、[
|