题目内容
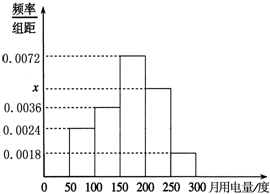从某小区抽取100户居民进行月用电量调查，发现其用电量都在50到300度之间，频率分布直方图所示，则在这些用户中，用电量落在区间[150，250）内的户数为（ ）| A、70 | B、61 | C、36 | D、25 |
考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图，先求出用电量在区间[150，250）内的频率，再求对应的频数即（户数）．
解答：
解：根据频率分布直方图，得：
用电量在区间[150，250）内的频率是：
1-（0.0024+0.0036+0.0018）×50=1-0.39=0.61，
∴频数即（户数）为
100×0.61=61．
故选：B．
用电量在区间[150，250）内的频率是：
1-（0.0024+0.0036+0.0018）×50=1-0.39=0.61，
∴频数即（户数）为
100×0.61=61．
故选：B．
点评：本题考查了频率分布直方图的应用问题，解题时应根据频率分布直方图，求出频率，再求频数，是基础题．
练习册系列答案
相关题目
函数f（x）=x3-3bx+3b在（0，1）内有极小值的充分不必要条件是（ ）
| A、b∈（0，1） | ||
| B、b∈（1，+∞） | ||
C、b∈（
| ||
| D、b∈（-∞，1） |
在等差数列{an}中，Sn表示前n项和，a1+a6=5，则S6=（ ）
| A、15 | B、18 | C、12 | D、16 |
执行如图所示的框图，如果输入的x∈[0，
]，则输出的y值属于（ ）
| π |
| 2 |
| A、[0，1] | ||||
B、[0，
| ||||
C、[
| ||||
D、[
|
已知a＞0，b＞0且a+2b=2，若
+
＞m恒成立，则实数m的取值范围为（ ）
| 2 |
| a |
| 1 |
| b |
| A、（-∞，8） |
| B、（8，+∞） |
| C、（-∞，4） |
| D、（4，+∞） |
已知经过同一点的n（n∈N*，n≥3）个平面，任意三个平面不经过同一条直线．若这n个平面将空间分成f（n）个部分，则f（n）=（ ）
A、
| ||
B、
| ||
| C、n2-n+1 | ||
| D、n2-n+2 |
已知数据（3，2.5），（4，3），（5，4），（6，4.5）线性相关，则其回归直线方程为（ ）
| A、y=0.7x+0.35 |
| B、y=x-3 |
| C、y=0.5x+0.3 |
| D、y=-0.4x+5.1 |
若
＜
＜0，则下列不等式：①|a|＞|b|；②a+b＞ab；③
+
＞2；④
＜2a-b中，正确的不等式是（ ）
| 1 |
| a |
| 1 |
| b |
| a |
| b |
| b |
| a |
| a2 |
| b |
| A、①② | B、③④ | C、①③ | D、②④ |