题目内容
13.正弦函数是奇函数,因为f(x)=sin(x+1)是正弦函数,所以f(x)=sin(x+1)是奇函数.以上推理( )| A. | 结论正确 | B. | 大前提错误 | C. | 小前提错误 | D. | 以上都不对 |
分析 根据题意,分析所给推理的三段论,找出大前提,小前提,结论,再判断正误即可得答案.
解答 解:根据题意,该推理的大前提:正弦函数是奇函数,正确;
小前提:f(x)=sin(x+1)是正弦函数,因为该函数f(x)=sin(x+1)不是正弦函数,故错误;
结论:f(x)=sin(x+1)是奇函数,故错误.
故选:C.
点评 本题考查演绎推理的基本方法,关键是理解演绎推理的定义以及三段论的形式.

练习册系列答案
相关题目
3.函数$y=sin(2x-\frac{π}{3})$的图象经过下列平移,所得图象对应的函数为偶函数的是( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{5π}{12}$个单位 | D. | 向右平移$\frac{5π}{12}$个单位 |
4.已知△ABC是等腰直角三角形,点E,F是斜边AC的三等分点,则tan∠EBF=( )
| A. | $\frac{16}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{3}{4}$ |
1.如图,已知向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$,那么下列结论正确的是( )
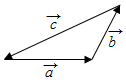

| A. | $\overrightarrow a+\overrightarrow b=\overrightarrow c$ | B. | $\overrightarrow a+\overrightarrow b=-\overrightarrow c$ | C. | $\overrightarrow a-\overrightarrow b=-\overrightarrow c$ | D. | $\overrightarrow b+\overrightarrow c=\overrightarrow a$ |
5.设x∈R,则“|x-1|<1”是“x2-x-2<0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.某舞步每一节共九步,且每一步各不相同,其中动作A三步,动作B三步,动作C三步,同一种动作相邻,则这种舞步一节中共有多少种不同的变化( )
| A. | 1296种 | B. | 216种 | C. | 864种 | D. | 1080种 |
6.在同一平面直角坐标系中,经过伸缩变换$\left\{\begin{array}{l}x′=5x\\ y′=3y\end{array}$后,曲线C变为曲线x′2+y′2=0,则曲线C的方程为( )
| A. | 25x2+9y2=0 | B. | 25x2+9y2=1 | C. | 9x2+25y2=0 | D. | 9x2+25y2=1 |