题目内容
14.点N是圆(x+5)2+y2=1上的动点,以点A(4,0)为直角顶点的Rt△ABC另外两个顶点B,C在圆x2+y2=40上,且BC的中点为M,则MN的最大值为8+2$\sqrt{6}$.分析 求出M的轨迹方程,得出圆心距,即可得出结论.
解答 解:由题意,MA=MC,
设M(x,y),则x2+y2+(x-4)2+y2=40,即(x-2)2+y2=24,表示以D(2,0)为圆心,2$\sqrt{6}$为半径的圆,
∵圆(x+5)2+y2=1的圆心与D的距离为:7,
∴|MN|的最大值为:7+1+2$\sqrt{6}$=8+2$\sqrt{6}$,
故答案为:8+2$\sqrt{6}$.
点评 本题考查轨迹方程,考查圆与圆的位置关系,考查学生转化问题的能力,属于中档题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
1.如图,已知向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$,那么下列结论正确的是( )
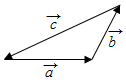

| A. | $\overrightarrow a+\overrightarrow b=\overrightarrow c$ | B. | $\overrightarrow a+\overrightarrow b=-\overrightarrow c$ | C. | $\overrightarrow a-\overrightarrow b=-\overrightarrow c$ | D. | $\overrightarrow b+\overrightarrow c=\overrightarrow a$ |
2.某舞步每一节共九步,且每一步各不相同,其中动作A三步,动作B三步,动作C三步,同一种动作相邻,则这种舞步一节中共有多少种不同的变化( )
| A. | 1296种 | B. | 216种 | C. | 864种 | D. | 1080种 |
2.某城市随机抽取一年内100天的空气质量指数(AQI)的监测数据,结果统计如表:
(1)若空气质量为严重污染则企业必须放假,试估计一年中(以360天计算)企业因为空气严重污染放假的天数;
(2)已知某企业每天的经济损失y(单位:元)与空气质量指数x的关系式为
y=$\left\{\begin{array}{l}{0,0≤x≤100}\\{4x-400,100<x≤300}\\{2000,x>300}\end{array}\right.$
1)若在本年内随机抽取一天,试估计这一天的经济损失超过400元的概率;
2)若以区间中点值计算空气质量指数,试估计一年中(以360天计算)企业因空气污染原因造成的经济损失是多少元.
| AQI | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数 | 6 | 14 | 18 | 27 | 20 | 15 |
(2)已知某企业每天的经济损失y(单位:元)与空气质量指数x的关系式为
y=$\left\{\begin{array}{l}{0,0≤x≤100}\\{4x-400,100<x≤300}\\{2000,x>300}\end{array}\right.$
1)若在本年内随机抽取一天,试估计这一天的经济损失超过400元的概率;
2)若以区间中点值计算空气质量指数,试估计一年中(以360天计算)企业因空气污染原因造成的经济损失是多少元.
9.定义a1=(1,1),a2=(1,2),a3=(2,1),a4=(1,3),a5=(2,2),a6=(3,1),…(n∈N*),则a2017=( )
| A. | (1,63) | B. | (63,1) | C. | (64,1) | D. | (1,64) |
19.2017年厦门航空公司在调查男女乘客140人是否晕机的情况中,已知男乘客60人,其中晕机为15人,女乘客80人,其中晕机为35人.
(1)根据以上的数据建立一个列联表
(2)能否在犯错误的概率不超过0.001的前提下认为晕机与性别有关
(1)给定临界值表
(2)${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
(1)根据以上的数据建立一个列联表
(2)能否在犯错误的概率不超过0.001的前提下认为晕机与性别有关
(1)给定临界值表
| P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
6.在同一平面直角坐标系中,经过伸缩变换$\left\{\begin{array}{l}x′=5x\\ y′=3y\end{array}$后,曲线C变为曲线x′2+y′2=0,则曲线C的方程为( )
| A. | 25x2+9y2=0 | B. | 25x2+9y2=1 | C. | 9x2+25y2=0 | D. | 9x2+25y2=1 |
3.观察数组:(-1,1,-1),(1,2,2),(3,4,12),(5,8,40),…,(an,bn,cn),则cn的值不可能为( )
| A. | 112 | B. | 278 | C. | 704 | D. | 1664 |
4.下列各点中,与点$(2,\frac{π}{6})$在极坐标系中表示同一个点的是( )
| A. | $(2,\frac{5π}{6})$ | B. | $(2,-\frac{π}{6})$ | C. | $(1,\frac{π}{6})$ | D. | $(2,\frac{13π}{6})$ |