题目内容
二项式(x-
)6的展开式中各项系数和与常数项分别为M,N,则
= .
| 2 | ||
|
| N |
| M |
考点:二项式定理的应用
专题:二项式定理
分析:令x=1,可得二项式(x-
)6的展开式中各项系数和M=1.再根据二项式(x-
)6的展开式的通项公式求得常数项N,可得
的值.
| 2 | ||
|
| 2 | ||
|
| N |
| M |
解答:
解:令x=1,可得二项式(x-
)6的展开式中各项系数和为1,M=1.
再根据二项式(x-
)6的展开式的通项公式为 Tr+1=
•(-2)r•x6-
r,令6-
r=0,求得r=4,可得常数项为N=
•16=240,
∴
=240,
故答案为:240.
| 2 | ||
|
再根据二项式(x-
| 2 | ||
|
| C | r 6 |
| 3 |
| 2 |
| 3 |
| 2 |
| C | 4 6 |
∴
| N |
| M |
故答案为:240.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中,锐角A满足sin4A-cos4A≤sinA-cosA,则( )
A、0<A≤
| ||||
B、0<A≤
| ||||
C、
| ||||
D、
|
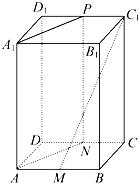 如图,长方体ABCD-A1B1C1D1中,M,N,P分别为线段AB,CD,C1D1的中点.求证:
如图,长方体ABCD-A1B1C1D1中,M,N,P分别为线段AB,CD,C1D1的中点.求证: 随着社会的发展,网上购物已成为一种新型的购物方式.某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价.以下为四款商品销售情况的条形图和用分层抽样法选取100份评价的统计表:
随着社会的发展,网上购物已成为一种新型的购物方式.某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价.以下为四款商品销售情况的条形图和用分层抽样法选取100份评价的统计表: