题目内容
已知曲线C:
+y2=1,直线l
(t为参数)
(1)以坐标原点为极点,x轴的正半轴为极轴建立直角坐标系,写出直线l的极坐标方程和曲线C的参数方程;
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
| x2 |
| 4 |
|
(1)以坐标原点为极点,x轴的正半轴为极轴建立直角坐标系,写出直线l的极坐标方程和曲线C的参数方程;
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
考点:直线的参数方程,直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由直线l
(t为参数),把x=t代入y=
-
t消去参数可得直角坐标方程,把
代入可得极坐标方程.由曲线C:
+y2=1,可得参数方程为
(α为参数,α∈[0,2π)).
(2)如图所示,设椭圆上的任意一点P(2cosα,sinα)(α∈[0,2π)).则点P到直线l的距离d=
=
,可得最大值,
因此|PA|的最大值为
.
|
| 2 |
| 3 |
|
| x2 |
| 4 |
|
(2)如图所示,设椭圆上的任意一点P(2cosα,sinα)(α∈[0,2π)).则点P到直线l的距离d=
|2
| ||||
| 2 |
|
| ||||
| 2 |
因此|PA|的最大值为
| d |
| sin30° |
解答:
解:(1)由直线l
(t为参数),消去参数化为y=
-
x,把
代入可得
ρcosθ+ρsinθ-
=0.
由曲线C:
+y2=1,可得参数方程为
(α为参数,α∈[0,2π)).
(2)如图所示,
过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,设椭圆上的任意一点P(2cosα,sinα)(α∈[0,2π)).
则点P到直线l的距离d=
=
≤
,
∴|PA|的最大值为
=
+
.
|
| 2 |
| 3 |
|
| 3 |
| 2 |
由曲线C:
| x2 |
| 4 |
|
(2)如图所示,

过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,设椭圆上的任意一点P(2cosα,sinα)(α∈[0,2π)).
则点P到直线l的距离d=
|2
| ||||
| 2 |
|
| ||||
| 2 |
| ||||
| 2 |
∴|PA|的最大值为
| ||||||
| sin30° |
| 13 |
| 2 |
点评:本题考查了直线的参数方程化为直角坐标方程、化为极坐标方程、点到直线的距离公式、直角三角形的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
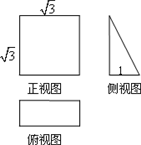 一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积为( )
一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积为( )A、
| ||
| B、1 | ||
C、
| ||
| D、3 |
已知△ABC是边长为2的正三角形,则
•
的值为( )
| AB |
| BC |
| A、2 | ||
| B、-2 | ||
C、2
| ||
D、-2
|