题目内容
四个数排成一串,已知前三个数成等差数列,后三个数成等比数列,且第二个数与第三个数之和为8,第一个数与第四个数之和为16,求这四个数.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:设这四个数为a,b,c,d,由已知得
,由此能求出这四个数.
|
解答:
解:设这四个数为a,b,c,d,
由已知得
,解得a=-2,b=2,c=6,d=18.
∴这四个数为:-2,2,6,18.
由已知得
|
∴这四个数为:-2,2,6,18.
点评:本题考查四个数的求法,是中档题,解题时要注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
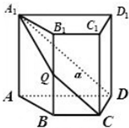 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则| B1Q |
| QB |
| A、1 | ||
| B、2 | ||
| C、3 | ||
D、与
|
设函数y=f(x)在R上有定义,对于任一给定的正数p,定义函数fp(x)=
,则称函数fp(x)为f(x)的“p界函数”,若给定函数f(x)=x2-2x-2,p=1,则下列结论成立的是( )
|
| A、fp[f(0)]=f[fp(0)] |
| B、fp[f(1)]=f[fp(1)] |
| C、fp[f(2)]=fp[fp(2)] |
| D、f[f(-2)]=fp[fp(-2)] |




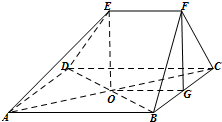 如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.
如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.