题目内容
12．若角α的终边经过点P（4，-3），则sinα=（ ）| A． | ±$\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | ±$\frac{4}{5}$ |
分析 由三角函数的定义可直接求得sinα．
解答 解：∵角a的终边经过点P（4，-3），
∴sinα=$\frac{-3}{\sqrt{16+9}}$=-$\frac{3}{5}$．
故选B．
点评 本题考查任意角的三角函数的定义，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
2．已知数列{an}是递增等差数列，且a1+a4=8，a2a3=15，设${b_n}=\frac{1}{{{a_n}•{a_{n+1}}}}$，则数列{bn}的前10项和为（ ）
| A． | $\frac{9}{19}$ | B． | $\frac{18}{19}$ | C． | $\frac{20}{21}$ | D． | $\frac{10}{21}$ |
20．执行图中程序框图，若输入x1=2，x2=3，x3=7，则输出的T值为（ ）
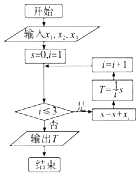
| A． | 3 | B． | 4 | C． | $\frac{11}{3}$ | D． | 5 |
7．双曲线C：$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的离心率为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{6}}{2}$ | C． | $\frac{\sqrt{2}}{4}$ | D． | $\frac{\sqrt{6}}{4}$ |
4．设数列{an}满足：a1=2，an+1=1-$\frac{1}{{a}_{n}}$，记数列{an}的前n项之积为T，则T2017的值为（ ）
| A． | -$\frac{1}{2}$ | B． | -1 | C． | 2 | D． | -2 |
1．下列函数中，既不是奇函数又不是偶函数的是（ ）
| A． | y=x2+|x| | B． | y=2x-2-x | C． | y=x2-3x | D． | y=$\frac{1}{x+1}$+$\frac{1}{x-1}$ |
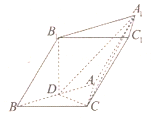如图，在三棱柱ABC-A1B1C1中，D为AB的中点，CD⊥DA1，AC⊥BC，∠ABB1=45°，AC=BC=BB1=2．