题目内容
18.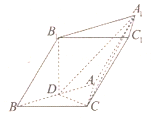 如图,在三棱柱ABC-A1B1C1中,D为AB的中点,CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.
如图,在三棱柱ABC-A1B1C1中,D为AB的中点,CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.(1)证明:B1D⊥BD;
(2)求点A到平面A1CD的距离.
分析 (1)推导出BD=$\frac{1}{2}$BA=$\sqrt{2}$,从而∠B1BD=90°,由此能证明B1D⊥BD.
(2)推导出CD⊥平面ABB1A,从而平面CDA1⊥平面ABB1A,过A作AE⊥DA1于E,则AE⊥平面A1DC,AE即为点A到平面A1CD的距离,由此利用等面积法能求出点A到平面A1CD的距离.
解答 (本小题满分12分)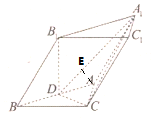
证明:(1)∵在三棱柱ABC-A1B1C1中,D为AB的中点,
CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.
∴BD=$\frac{1}{2}$BA=$\sqrt{2}$,…(2分)
又BB1=2,且∠B1BD=45°,∴∠B1BD=90°,
∴B1D⊥BD.…(6分)
解:(2)∵CD⊥BA,CD⊥DA1,∴CD⊥平面ABB1A,
∴平面CDA1⊥平面ABB1A,…(8分)
过A作AE⊥DA1于E,则AE⊥平面A1DC,∴AE即为点A到平面A1CD的距离,…(10分)
A1D=$\sqrt{{B}_{1}{D}^{2}+{B}_{1}{{A}_{1}}^{2}}$=$\sqrt{10}$,
故在△ADA1中,
由等面积法得AE=$\frac{\sqrt{2}×\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{10}}{5}$.…(12分)
点评 本题考查线线垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
12.若角α的终边经过点P(4,-3),则sinα=( )
| A. | ±$\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | ±$\frac{4}{5}$ |
9.利用独立性检验考察两个分类变量X与Y是否有关系时,若K2的观测值k=6.132,则有97.5%的把握认为“X与Y有关系”.
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
6.双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的左右焦点分别为F1,F2,P是双曲线上的点,且∠F1PF2=90°,则△F1PF2的面积S=( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
13.焦点在y轴上,虚半轴的长为4,半焦距为6的双曲线的标准方程为( )
| A. | $\frac{{y}^{2}}{20}$-$\frac{{x}^{2}}{16}$=1 | B. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{20}$=1 | C. | $\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{36}$=1 | D. | $\frac{{y}^{2}}{36}$-$\frac{{x}^{2}}{16}$=1 |
3.已知在△ABC中,角A,B,C分别为△ABC的三个内角,若命题p:sinA>sinB,命题q:A>B,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |