题目内容
已知函数y=3x+
的图象上有一点列P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),其中数列{xn}为等差数列,满足x2=-
,x5=-
.
(Ⅰ)求点Pn的坐标;
(Ⅱ)若抛物线列C1,C2,…,Cn分别以点P1,P2,…,Pn为顶点,且任意一条的对称轴均平行于y轴,Cn与y轴的交点为An(0,n2+1),记与抛物线Cn相切于点An的直线的斜率为kn,求数列{
}前n项的和Sn.
| 13 |
| 4 |
| 7 |
| 2 |
| 13 |
| 2 |
(Ⅰ)求点Pn的坐标;
(Ⅱ)若抛物线列C1,C2,…,Cn分别以点P1,P2,…,Pn为顶点,且任意一条的对称轴均平行于y轴,Cn与y轴的交点为An(0,n2+1),记与抛物线Cn相切于点An的直线的斜率为kn,求数列{
| 1 |
| kn+1kn |
考点:数列的求和,数列与函数的综合
专题:等差数列与等比数列
分析:(I)设等差数列{xn}的公差为d,可得d=
,利用等差数列的通项公式可得xn,进而得到yn.
(II)由题意可设以Pn为顶点的抛物线Cn的方程为:y=a(x+
)2-
,由于Cn与y轴的交点为An(0,n2+1),代入解得a=1,可得以Pn为顶点的抛物线方程为:y=(x+
)2-
,利用导数的几何意义可得切线的斜率,再利用“裂项求和”即可得出Sn.
| x5-x2 |
| 3 |
(II)由题意可设以Pn为顶点的抛物线Cn的方程为:y=a(x+
| 2n+3 |
| 2 |
| 5+12n |
| 4 |
| 2n+3 |
| 2 |
| 5+12n |
| 4 |
解答:
解:(I)设等差数列{xn}的公差为d,
∵x2=-
,x5=-
,
∴d=
=
=-1.
∴xn=x2+(n-2)d=-
-(n-2)=-
.
∴yn=3xn+
=-
.
∴Pn(-
,-
).
(II)由题意可设以Pn为顶点的抛物线方程为:y=a(x+
)2-
,
∵Cn与y轴的交点为An(0,n2+1),
∴n2+1=a(
)2-
,
解得a=1,
∴以Pn为顶点的抛物线方程为:y=(x+
)2-
,
y′=2(x+
),
∴y′(x=0)=2n+3=kn,
∴kn+1=2n+5.
∴
=
=
(
-
),
∴数列{
}前n项的和Sn=
[(
-
)+(
-
)+…+(
-
)]
=
(
-
)
=
.
∵x2=-
| 7 |
| 2 |
| 13 |
| 2 |
∴d=
| x5-x2 |
| 3 |
-
| ||||
| 3 |
∴xn=x2+(n-2)d=-
| 7 |
| 2 |
| 2n+3 |
| 2 |
∴yn=3xn+
| 13 |
| 4 |
| 5+12n |
| 4 |
∴Pn(-
| 2n+3 |
| 2 |
| 5+12n |
| 4 |
(II)由题意可设以Pn为顶点的抛物线方程为:y=a(x+
| 2n+3 |
| 2 |
| 5+12n |
| 4 |
∵Cn与y轴的交点为An(0,n2+1),
∴n2+1=a(
| 2n+3 |
| 2 |
| 5+12n |
| 4 |
解得a=1,
∴以Pn为顶点的抛物线方程为:y=(x+
| 2n+3 |
| 2 |
| 5+12n |
| 4 |
y′=2(x+
| 2n+3 |
| 2 |
∴y′(x=0)=2n+3=kn,
∴kn+1=2n+5.
∴
| 1 |
| kn•kn+1 |
| 1 |
| (2n+3)(2n+5) |
| 1 |
| 2 |
| 1 |
| 2n+3 |
| 1 |
| 2n+5 |
∴数列{
| 1 |
| kn+1kn |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2n+3 |
| 1 |
| 2n+5 |
=
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 2n+5 |
=
| n |
| 10n+25 |
点评:本题考查了等差数列的通项公式及其性质、抛物线的标准方程及其性质、导数的几何意义、抛物线的切线方程、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
设集合M={x|x2-2x<0},N={x||x|≤1},则M∩N=( )
| A、[-1,0) |
| B、(-2,-1] |
| C、(0,1] |
| D、(0,2) |
观察下面频率等高条形图,其中两个分类变量C之间关系最强的是( )
A、 |
B、 |
C、 |
D、 |
已知双曲线
-
=1(a>0,b>0)的离心率e=2,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
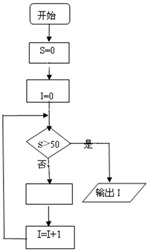 程序框图,如图所示为1+2+3+…+n>50的最小自然数n的程序框图,在空白框中应填
程序框图,如图所示为1+2+3+…+n>50的最小自然数n的程序框图,在空白框中应填