题目内容
设集合M={x|x2-2x＜0}，N={x||x|≤1}，则M∩N=（ ）
| A、[-1，0） |
| B、（-2，-1] |
| C、（0，1] |
| D、（0，2） |
考点：交集及其运算
专题：集合
分析：求出M与N中不等式的解集确定M与N，求出两集合的交集即可．
解答：
解：由M中不等式变形得：x（x-2）＜0，
解得：0＜x＜2，即M=（0，2），
由N中不等式解得：-1≤x≤1，即N=[-1，1]，
则M∩N=（0，1]，
故选：C．
解得：0＜x＜2，即M=（0，2），
由N中不等式解得：-1≤x≤1，即N=[-1，1]，
则M∩N=（0，1]，
故选：C．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
三角函数f（x）=asinx-bcosx，若f（
-x）=f（
+x），则直线ax-by+c=0的倾斜角为（ ）
| π |
| 4 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设全集U={x|x≥3，x∈N}，集合A={x|x2≥10，x∈N}．则∁UA=（ ）
| A、∅ |
| B、{3} |
| C、{10} |
| D、{3，4，5，6，7，8，9} |
设0＜α＜
，a是大于0的常数，函数F（α）=
+
，若F（α）≥16恒成立，则a的取值范围是（ ）
| π |
| 2 |
| 1 |
| cosα |
| a |
| 1-cosα |
| A、[1，+∞） |
| B、[4，+∞） |
| C、（9，+∞） |
| D、[9，+∞） |
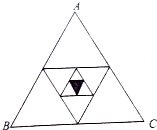如图，等边三角形ABC，以△ABC各边中点为顶点作三角形，以此类推，现向△ABC中随机撒入320颗豆子，则落在阴影部分内的豆子大约是