题目内容
设数列{an}满足a1=0且an+1=
.n∈N*.
(1)求证数列{
}是等差数列,并求数列{an}的通项公式;
(2)设bn=
,Sn为数列{bn}的前n项和,证明:Sn<1.
| 1 |
| 2-an |
(1)求证数列{
| 1 |
| 1-an |
(2)设bn=
1-
| ||
|
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)把an+1=
代入
-
,能推导出
-
=1,由此能证明数列{
}是公差为1的等差数列,从而能求出an=1-
.
(2)由bn=
=
=
-
,利用裂项求和法能证明Sn<1.
| 1 |
| 2-an |
| 1 |
| 1-an+1 |
| 1 |
| 1-an |
| 1 |
| 1-an+1 |
| 1 |
| 1-an |
| 1 |
| 1-an |
| 1 |
| n |
(2)由bn=
1-
| ||
|
| ||||
|
| 1 | ||
|
| 1 | ||
|
解答:
(1)解:∵an+1=
,
∴
-
=
-
=
-
=1,
∴
-
=1,
∴数列{
}是公差为1的等差数列.
又
=1, 故
=n,
所以an=1-
.
(2)证明:由(1)得bn=
=
=
-
,Sn=
bk=
(
-
)=1-
<1.
∴Sn<1.
| 1 |
| 2-an |
∴
| 1 |
| 1-an+1 |
| 1 |
| 1-an |
| 1 | ||
1-
|
| 1 |
| 2-an |
| 2-an |
| 1-an |
| 1 |
| 2-an |
∴
| 1 |
| 1-an+1 |
| 1 |
| 1-an |
∴数列{
| 1 |
| 1-an |
又
| 1 |
| 1-a1 |
| 1 |
| 1-an |
所以an=1-
| 1 |
| n |
(2)证明:由(1)得bn=
1-
| ||
|
| ||||
|
| 1 | ||
|
| 1 | ||
|
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
∴Sn<1.
点评:本题主要考查数列的通项公式、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查等差数列的证明,证明数列为等差数列通常利用等差数列的定义证明,遇到与数列的和有关的不等式可先考虑能否求和再证明.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
函数y=x(|x|-1)的图象是( )
A、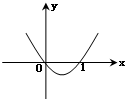 |
B、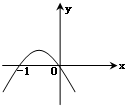 |
C、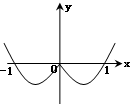 |
D、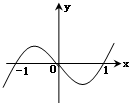 |
设0<α<
,a是大于0的常数,函数F(α)=
+
,若F(α)≥16恒成立,则a的取值范围是( )
| π |
| 2 |
| 1 |
| cosα |
| a |
| 1-cosα |
| A、[1,+∞) |
| B、[4,+∞) |
| C、(9,+∞) |
| D、[9,+∞) |