题目内容
经过点A(3,1)作直线l,它与双曲线
-y2=1只有一个公共点,这样的直线l有 条.
| x2 |
| 9 |
考点:双曲线的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:分为两类考虑:直线的斜率不存在;与渐近线平行的直线,即可得到结论.
解答:
解:①当直线l的斜率不存在时,直线的方程为x=3,直线与双曲线相切,满足题意;
②因为a=3,b=1,所以双曲线的渐近线方程为y=±
x,
则A在渐近线y=
x上,可作出一条与渐近线y=-
x平行的直线,即与双曲线只有一个交点;
故满足条件的直线共有2条.
故答案为:2.
②因为a=3,b=1,所以双曲线的渐近线方程为y=±
| 1 |
| 3 |
则A在渐近线y=
| 1 |
| 3 |
| 1 |
| 3 |
故满足条件的直线共有2条.
故答案为:2.
点评:本题考查了直线与双曲线有一个公共点的情况,做题时极容易丢平行渐近线的情况,做题时一定要细心.属于基础题型.

练习册系列答案
相关题目
函数y=x(|x|-1)的图象是( )
A、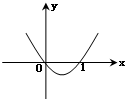 |
B、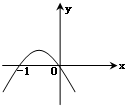 |
C、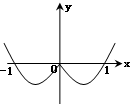 |
D、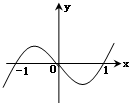 |
若
=
,则tan2α=( )
| 1+cos2α |
| sin2α |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
三角函数f(x)=asinx-bcosx,若f(
-x)=f(
+x),则直线ax-by+c=0的倾斜角为( )
| π |
| 4 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|