题目内容
已知双曲线
-
=1(a>0,b>0)的离心率e=2,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出抛物线的准线,即有双曲线的c=6,再由离心率公式和a2+b2=c2,可得a,b,即可得到双曲线方程.
解答:
解:抛物线y2=24x的准线为x=-6,
则有双曲线的一个焦点为(-6,0),
即c=6,
由e=
=2,可得a=3,
则b=
=
=3
.
即有双曲线的方程为
-
=1.
故选:B.
则有双曲线的一个焦点为(-6,0),
即c=6,
由e=
| c |
| a |
则b=
| c2-a2 |
| 36-9 |
| 3 |
即有双曲线的方程为
| x2 |
| 9 |
| y2 |
| 27 |
故选:B.
点评:本题考查抛物线和双曲线的方程和性质,运用离心率公式和a,b,c的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=|lg(x-1)|,若a≠b,f(a)=f(b),则a+2b的取值范围是( )
A、(4
| ||
B、[4
| ||
C、(2
| ||
D、[2
|
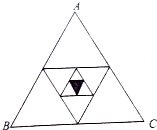 如图,等边三角形ABC,以△ABC各边中点为顶点作三角形,以此类推,现向△ABC中随机撒入320颗豆子,则落在阴影部分内的豆子大约是
如图,等边三角形ABC,以△ABC各边中点为顶点作三角形,以此类推,现向△ABC中随机撒入320颗豆子,则落在阴影部分内的豆子大约是