题目内容
已知a,b,c∈R,下列命题中正确的是( )
| A、a>b⇒ac2>bc2 | ||||
| B、ac2>bc2⇒a>b | ||||
C、a3>b3⇒
| ||||
| D、a2>b2⇒a>|b| |
考点:不等式的基本性质
专题:不等式的解法及应用
分析:A.取c=0时,即可判断出;
B.利用不等式的性质即可得出;
C.取a=1,b=-2,即可判断出;
D.取a=-2,b=1,即可判断出.
B.利用不等式的性质即可得出;
C.取a=1,b=-2,即可判断出;
D.取a=-2,b=1,即可判断出.
解答:
解:A.取c=0时,ac2=bc2=0,因此不正确;
B.∵ac2>bc2,∴a>b,正确;
C.取a=1,b=-2,满足a3>b3,但是a=
=1>
=
,因此不正确;
D.取a=-2,b=1,满足a2>b2,但是a<|b|,因此不正确.
综上可知:只有B正确.
故选:B.
B.∵ac2>bc2,∴a>b,正确;
C.取a=1,b=-2,满足a3>b3,但是a=
| 1 |
| a |
| 1 |
| -2 |
| 1 |
| b |
D.取a=-2,b=1,满足a2>b2,但是a<|b|,因此不正确.
综上可知:只有B正确.
故选:B.
点评:本题考查了不等式的基本性质、举反例否定一个命题的方法,属于基础题.

练习册系列答案
相关题目
定义a⊕b=
,设函数f(x)=lnx⊕x,则f(2)+f(
)=( )
|
| 1 |
| 2 |
| A、4ln2 | B、-4ln2 |
| C、2 | D、0 |
已知0<x<4.5,当x2(9-2x)取得最大值时,x取何值( )
| A、1 | B、2 | C、3 | D、27 |
下列不等式可以推出a>b的是( )
| A、ac>bc | ||||
B、
| ||||
| C、a+c>b+d | ||||
| D、a-c>b-c |
如果α在第二象限,则
必定在( )
| α |
| 2 |
| A、第一或第二象限 |
| B、第一或第三象限 |
| C、第三或第四象限 |
| D、第二或第四象限 |
如图所示计算机程序的打印结果为( )
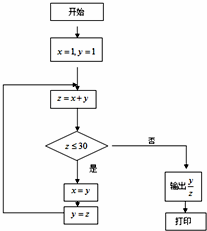

A、
| ||
B、
| ||
C、
| ||
D、
|
若x=
,则sin4x-cos4x的值为( )
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|