题目内容
7.已知集合$A=\{x|{(x-1)^2}≤\frac{3}{2}x-\frac{1}{2},x∈R\}$,B=N,则集合A∩B的真子集个数为( )| A. | 3 | B. | 4 | C. | 7 | D. | 8 |
分析 解不等式求出集合A,进而得到集合A∩B的元素个数,最后由n元集合有2n-1个真子集得到答案.
解答 解:∵集合$A=\{x|{(x-1)^2}≤\frac{3}{2}x-\frac{1}{2},x∈R\}$=[$\frac{1}{2}$,3],B=N,
∴集合A∩B={1,2,3},
故集合A∩B的真子集个数为23-1=7个,
故选:C.
点评 本题考查的知识点集合的交集运算,集合的真子集,难度中档.

练习册系列答案
相关题目
18.设集合M={x|x2-11x+10=0},N={y|y=lgx,x∈M},则M∩N=( )
| A. | {0,1} | B. | {0,1,10} | C. | {1} | D. | ∅ |
19.抛物线x2=-2y的焦点坐标为( )
| A. | $(0,-\frac{1}{8})$ | B. | $(-\frac{1}{8},0)$ | C. | $(0,-\frac{1}{2})$ | D. | $(-\frac{1}{2},0)$ |
17.在△ABC中,设D为BC的中点,则3$\overrightarrow{AB}$+2$\overrightarrow{BC}$+$\overrightarrow{CA}$=( )
| A. | $\overrightarrow{AD}$ | B. | 2$\overrightarrow{AD}$ | C. | 3$\overrightarrow{AD}$ | D. | 4$\overrightarrow{AD}$ |
 如图,E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA上的点如果四边形EFGH为平行四边形,求证:AC∥平面EFGH.
如图,E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA上的点如果四边形EFGH为平行四边形,求证:AC∥平面EFGH.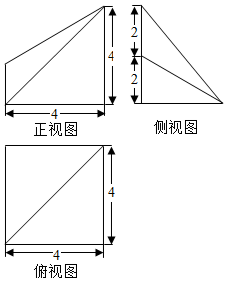 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{80}{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{80}{3}$.