题目内容
16．求使2sinx-3a=1成立的a的取值范围．分析 原方程可化为sinx=$\frac{1}{2}$（1+3a），由-1≤sinx≤1可得-1≤$\frac{1}{2}$（1+3a）≤1，解不等式组可得a的范围．
解答 解：方程2sinx-3a=1可化为sinx=$\frac{1}{2}$（1+3a），
由-1≤sinx≤1可得-1≤$\frac{1}{2}$（1+3a）≤1，
解不等式组可得-1≤a≤$\frac{1}{3}$．
点评 本题考查正弦函数的值域和不等式的解集，属基础题．
练习册系列答案
相关题目
1．在（x+$\frac{1}{x}$）4（2x-1）6的展开式中，常数项为（ ）
| A． | 6 | B． | 240 | C． | 480 | D． | 486 |
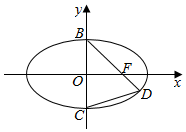如图，在平面直角坐标系xOy中，F为椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，B，C分别为椭圆的上、下顶点，直线BF与椭圆的另一个交点为D，且直线CD的斜率为$\frac{1}{2}$，则该椭圆的离心率为$\frac{\sqrt{2}}{2}$．