题目内容
17．在△ABC中，设D为BC的中点，则3$\overrightarrow{AB}$+2$\overrightarrow{BC}$+$\overrightarrow{CA}$=（ ）| A． | $\overrightarrow{AD}$ | B． | 2$\overrightarrow{AD}$ | C． | 3$\overrightarrow{AD}$ | D． | 4$\overrightarrow{AD}$ |
分析 化简3$\overrightarrow{AB}$+2$\overrightarrow{BC}$+$\overrightarrow{CA}$=2（$\overrightarrow{AB}$+$\overrightarrow{BC}$）+（$\overrightarrow{CA}$+$\overrightarrow{AB}$）=2$\overrightarrow{AC}$+$\overrightarrow{CB}$=$\overrightarrow{AC}$+$\overrightarrow{AB}$，从而解得．
解答 解：3$\overrightarrow{AB}$+2$\overrightarrow{BC}$+$\overrightarrow{CA}$=2（$\overrightarrow{AB}$+$\overrightarrow{BC}$）+（$\overrightarrow{CA}$+$\overrightarrow{AB}$）
=2$\overrightarrow{AC}$+$\overrightarrow{CB}$=$\overrightarrow{AC}$+$\overrightarrow{AB}$，
∵D为BC的中点，
∴$\overrightarrow{AC}$+$\overrightarrow{AB}$=2$\overrightarrow{AD}$，
故选：B．
点评 本题考查了平面向量的线性运算的应用及数形结合的思想应用．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
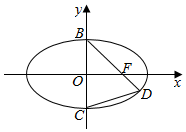如图，在平面直角坐标系xOy中，F为椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，B，C分别为椭圆的上、下顶点，直线BF与椭圆的另一个交点为D，且直线CD的斜率为$\frac{1}{2}$，则该椭圆的离心率为$\frac{\sqrt{2}}{2}$．
5．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线过曲线y=x2-4x+1的最低点，则该双曲线的离心率e的值是（ ）
| A． | $\frac{\sqrt{15}}{3}$ | B． | $\frac{\sqrt{13}}{3}$ | C． | $\frac{\sqrt{13}}{2}$ | D． | $\frac{\sqrt{15}}{2}$ |