Question

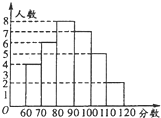某中学部分学生参加全国高中数学竞赛取得了优异成绩，指导老师统计了所有参赛同学的成绩（成绩都为整数，试题满分120分），并且绘制了“频数分布直方图”，请回答：
（1）该中学参加本次数学竞赛的有多少人？
（2）如果90分以上（含90分）获奖，那么获奖率是多少？
（3）这次竞赛成绩的中位数和众数分别落在哪个分数段内？请说明理由．

Answer 1

考点：频率分布直方图,众数、中位数、平均数

专题：概率与统计

分析：（1）由直方图，求出各分数段内的频数和即可；
（2）求出90（含90分）以上的人数，再求获奖率；
（3）根据直方图中各分数段内的频数，结合中位数与众数的概念，即可得出结论．

解答： 解：（1）由直方图知，参加本次竞赛的有：
4+6+8+7+5+2=32（人）；
（2）90（含90分）以上的人数为
7+5=2=14，
∴

14

32

×100%=43.75%，
即本次竞赛获奖率是43.75%；
（3）参赛同学共有32人，按成绩排序后，第16，17个数是最中间两个，
即中位数落在80～90之间；
由直方图，落在80～90之间的人数最多，共8人，
∴众数也落在80～90之间．

点评：本题考查了频率分布直方图的应用问题，解题时应根据直方图中的数据进行解答，是基础题．