题目内容
已知A，B，C为△ABC的三个内角，且∠A＜∠B＜∠C，sinB=
，cos（2A+C）=-
，求cos2A的值．
| 4 |
| 5 |
| 4 |
| 5 |
考点：两角和与差的余弦函数
专题：计算题,三角函数的求值
分析：由已知可先得cos（B-A）=
，sin（B-A）=
，cosB=
，从而再求得sinA的值，即可求出cos2A的值．
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
解答：
解：∵cos（2A+C）=cos（A+π-B）=-
，
∴cos（B-A）=
，
∵A，B，C为△ABC的三个内角，且∠A＜∠B＜∠C，
∴sin（B-A）=
，cosB=
，
∴sinA=sin[B-（B-A）]=sinBcos（B-A）-cosBsin（B-A）=
×
-
×
=
cos2A=1-2sin2A=1-2×(
)2=
| 4 |
| 5 |
∴cos（B-A）=
| 4 |
| 5 |
∵A，B，C为△ABC的三个内角，且∠A＜∠B＜∠C，
∴sin（B-A）=
| 3 |
| 5 |
| 3 |
| 5 |
∴sinA=sin[B-（B-A）]=sinBcos（B-A）-cosBsin（B-A）=
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 7 |
| 25 |
cos2A=1-2sin2A=1-2×(
| 7 |
| 25 |
| 527 |
| 625 |
点评：本题主要考察了两角和与差的余弦函数，三角函数的求值，属于基本知识的考查．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
已知定义在[1-2a，2-a]上的偶函数f（x），当x≥0时，f（x）=x+ex，若f（t）＜f（2t-1）．则t的取值范围是（ ）
| A、[-1，1] | ||
| B、[0，1] | ||
C、[
| ||
D、[0，
|
如图，已知PA⊥平面ABC，AD⊥BC于D，BC=CD=AD=1．记∠BPC=θ，则当PD=直线l经过P（1，1）且与双曲线x2-
=1交于A、B两点，如果点P是线段AB的中点，那么直线l的方程为（ ）
| y2 |
| 2 |
| A、2x-y-1=0 |
| B、2x+y-3=0 |
| C、x-2y+1=0 |
| D、不存在 |
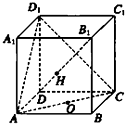如图，在正方体ABCD-A1B1C1D1中，O为正方形ABCD的中心，H为直线B1D与平面ACD1的交点，求证：D1、H、0三点共线．