题目内容
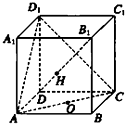如图，在正方体ABCD-A1B1C1D1中，O为正方形ABCD的中心，H为直线B1D与平面ACD1的交点，求证：D1、H、0三点共线．考点：平面的基本性质及推论
专题：空间位置关系与距离
分析：将三点共线转化为证两面的交线问题，利用两面相交，有且只有一条交线，即两面的公共点都共线证明．
解答：
证明：∵正方形ABCD的中心O是对角线AC、BD的交点，
∴D1O是平面ACD1与平面BB1D1D的交线，
又∵B1D在平面BB1D1D中，B1D与平面ACD1相交，
∴交点H在交线D1O上，
即D1、H、O．
∴D1O是平面ACD1与平面BB1D1D的交线，
又∵B1D在平面BB1D1D中，B1D与平面ACD1相交，
∴交点H在交线D1O上，
即D1、H、O．
点评：本题考查空间中的三点共线问题，转化求解，利用转化的思想求解，是数学中一类重要方法．
练习册系列答案
相关题目
已知方程kx+3-2k=
有两个不同的解，则实数k的取值范围是（ ）
| 4-x2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(0，
|
用a，b表示两条不同的直线，γ表示平面，给出下列命题：
（1）若a∥γ，b∥γ，则a∥b
（2）若a∥b，b∥γ，则a∥γ
（3）若a⊥γ，b∥γ，则a⊥b
（4）若a⊥γ，b⊥γ，则a∥b
其中真命题的序号是（ ）
（1）若a∥γ，b∥γ，则a∥b
（2）若a∥b，b∥γ，则a∥γ
（3）若a⊥γ，b∥γ，则a⊥b
（4）若a⊥γ，b⊥γ，则a∥b
其中真命题的序号是（ ）
| A、（1）（4） |
| B、（2）（3） |
| C、（3）（4） |
| D、（1）（2） |
圆台的上、下底面半径分别是10cm、20cm，它的侧面展开图--扇环的圆心角为180°，那么圆台的表面积是多少？（结果中保留π）