��Ŀ����
10���±��ṩ��ij�����ܽ��ļ�������������ײ�Ʒ�����м�¼�IJ���x���֣�����Ӧ�������ܺ�y���֣���ú�ļ���������ݣ�| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 2.5 | 3 | 4 | 4.5 | 5.22 | 5.97 |
��2����������0.05�������£�����x=7ʱ��x=8�����飨1������ع�ֱ���Ƿ���ʣ�
��3����֪�ó���������ǰ100�ּײ�Ʒ�ܺ�Ϊ90�ֱ�ú���Ը��ݣ�1����������Իع鷽�̣�Ԥ������100�ּײ�Ʒ�������ܺıȼ�������ǰ���Ͷ��ٶֱ�ú��
���ο���ʽ��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$��$\stackrel{��}{a}$=$\overline{y}$-b$\overline{x}$��
���� ��1�����ݱ���ֱ����x��y��ƽ���������ϵ��$\widehat{b}$��$\widehat{a}$��ֵ������ع鷽�̼��ɣ�
��2���ֱ�x=7��8���뷽���������жϼ��ɣ�
��3����x��ֵ�������ʽ���㼴�ɣ�
��� �⣺��1��$\overline{x}$=4.5��$\overline{y}$=3.5
$\stackrel{��}{b}$=$\frac{3.5}{5}$=0.7��$\widehat{a}$=0.35��
����$\stackrel{��}{y}$=0.7x+0.35��
��2���ɣ�1����֪��
��x=7ʱ��y=5.25��5.25-5.22=0.03��0.05
��x=8ʱ��y=5.95��5.97-5.95=0.02��0.05
���ԣ��˻ع�ֱ�߷���������
��3���ɣ�1����֪����x=100ʱ��y=70.35���֣�
���ԣ�������90-70.35=19.65�֣�
���� ���⿼���˻ع鷽�������Լ��ع鷽�̵�Ӧ�ã����������������һ���е��⣮

��ϰ��ϵ�д�
 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
��ѧ�����ϵ�д�
�����Ŀ
1��ij�༶Ҫ����������������Ů����ѡ�����˲μ�ij��������������ѡ��������������һ��Ů����ѡ��Ϊ��������
| A�� | 14 | B�� | 8 | C�� | 6 | D�� | 4 |
18��������y2=64x���߷���Ϊ��������
| A�� | x=8 | B�� | x=-8 | C�� | x=-16 | D�� | x=16 |
5�����к����У���СֵΪ2�ĺ����ǣ�������
| A�� | y=x+$\frac{1}{x}$ | B�� | y=sin��+$\frac{1}{sin��}$��0���ȣ�$\frac{��}{2}$�� | ||
| C�� | y=sin��+$\frac{1}{sin��}$��0���ȣ��У� | D�� | $\frac{1}{{\sqrt{{x^2}+2}}}+\sqrt{{x^2}+2}$ |
19����������y2=4x�Ľ�������x�ᴹֱ��ֱ�߽�˫����${x^2}-\frac{y^2}{3}=1$��������������A��B���㣬��AB=��������
| A�� | $\frac{{4\sqrt{3}}}{3}$ | B�� | $2\sqrt{3}$ | C�� | 6 | D�� | $4\sqrt{3}$ |
 ��ͼ����P-ABCD�ĵ���ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=2��BD=$2\sqrt{2}$��������P-BC-D����ֵ�Ĵ�С��
��ͼ����P-ABCD�ĵ���ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=2��BD=$2\sqrt{2}$��������P-BC-D����ֵ�Ĵ�С�� ��
�� ������
������ �ļ�ֵ�͵������䣻
�ļ�ֵ�͵������䣻 �����ٴ���һ��
�����ٴ���һ�� ��ʹ��
��ʹ��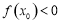 ��������ʵ��
��������ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ��