题目内容
已知双曲线C:
-
=1(a>0,b>0)的一条渐近线为y=
x,抛物线y2=24x的准线经过双曲线C的一个焦点,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、2 | ||
| B、3 | ||
C、2
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由抛物线标准方程易得其准线方程为x=-6,可得双曲线的左焦点为(-6,0),再根据焦点在x轴上的双曲线的渐近线方程,得a、b的另一个方程,运用离心率公式即可得到.
解答:
解:因为抛物线y2=24x的准线方程为x=-6,
所以由题意知,点F(-6,0)是双曲线的左焦点,
所以a2+b2=c2=36,①
又双曲线的一条渐近线方程是y=
x,
所以
=
,②
由①②解得a2=9,b2=27,
所以双曲线的离心率为
=
=2.
故选A.
所以由题意知,点F(-6,0)是双曲线的左焦点,
所以a2+b2=c2=36,①
又双曲线的一条渐近线方程是y=
| 3 |
所以
| b |
| a |
| 3 |
由①②解得a2=9,b2=27,
所以双曲线的离心率为
| c |
| a |
| 6 |
| 3 |
故选A.
点评:本题主要考查双曲线和抛物线的标准方程与几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
与两条异面直线分别相交的两条直线( )
| A、可能是平行直线 |
| B、一定是异面直线 |
| C、可能是相交直线 |
| D、一定是相交直线 |
如图是某几何体的三视图,则该几何体的外接球的表面积为( )


| A、200π | B、150π |
| C、100π | D、50π |
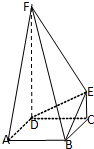 如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.
如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°. 如图所示,在长方体 A BCD-A′B′C′D′中,|A B|=λ|AD|=λ|A A′|(λ>0),E、F分别是 A′C′和 AD的中点,且 EF⊥平面 A′BCD′.
如图所示,在长方体 A BCD-A′B′C′D′中,|A B|=λ|AD|=λ|A A′|(λ>0),E、F分别是 A′C′和 AD的中点,且 EF⊥平面 A′BCD′.