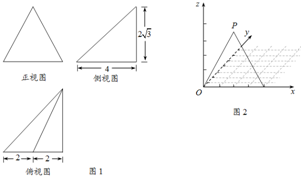
题目内容
y=arcsin2x-arccotx的值域 .
考点:反三角函数的运用
专题:计算题,函数的性质及应用
分析:先求出函数的定义域,再判断函数的单调性,根据单调性求最值.
解答:
解:由题意知-1≤2x≤1,解得:-
≤x≤
,
即函数的定义域为[-
,
];
所以arcsin2x是增函数,-arccotx也是增函数,
所以y=arcsin2x-arccotx是增函数,
所以当x=
时,函数有最大值,为
-arccot
;
当x=-
时,函数有最小值,为-
-arccot(-
),
所以值域为[-
-arccot(-
),
-arccot
],
故答案为:[-
-arccot(-
),
-arccot
].
| 1 |
| 2 |
| 1 |
| 2 |
即函数的定义域为[-
| 1 |
| 2 |
| 1 |
| 2 |
所以arcsin2x是增函数,-arccotx也是增函数,
所以y=arcsin2x-arccotx是增函数,
所以当x=
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
当x=-
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
所以值域为[-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
故答案为:[-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
点评:该题考查三角函数的反函数值域,属难题,解答该题时要注意三角函数的图象与其反函数的图象关于y=x对称.

练习册系列答案
相关题目
已知集合A={1,2,3},B={2,4},则A∩B=( )
| A、{1} |
| B、{2} |
| C、{1,2} |
| D、{1,2,3,4} |
设变量x、y满足
,则目标函数z=2x+3y的最小值为( )
|
| A、7 | B、8 | C、22 | D、23 |
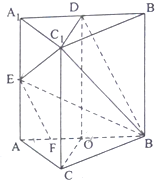 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1,侧棱AA1⊥平面ABC,O、D、E分别是棱AB、A1B1、AA1的中点,点F在棱AB上,且AF=
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1,侧棱AA1⊥平面ABC,O、D、E分别是棱AB、A1B1、AA1的中点,点F在棱AB上,且AF=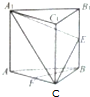 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.