题目内容
给出以下五个结论:
①函数f(x)=x
-(
)x的零点在区间(
,
)内;
②平面内的动点P到点F(-2,3)和到直线l:2x+y+1=0的距离相等,则点P的轨迹为抛物线;
③?x>0,不等式2x+
≥4成立的充要条件a≥2;
④若将函数f(x)=sin(2x-
)的图象向右平移φ(φ>0)个单位后变为偶函数,则φ的最小值是
;
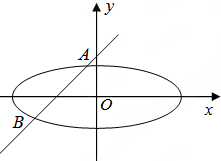
⑤过M(2,0)的直线l与椭圆
+y2=1交于P1,P2两点,线段P1P2中点为P,设直线l的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2等于-
,
其中正确结论的个数是( )
①函数f(x)=x
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
②平面内的动点P到点F(-2,3)和到直线l:2x+y+1=0的距离相等,则点P的轨迹为抛物线;
③?x>0,不等式2x+
| a |
| x |
④若将函数f(x)=sin(2x-
| π |
| 3 |
| π |
| 12 |
⑤过M(2,0)的直线l与椭圆
| x2 |
| 2 |
| 1 |
| 2 |
其中正确结论的个数是( )
| A、2 | B、3 | C、4 | D、5 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用幂函数与指数函数的单调性、函数零点的判定定理即可判断出;
②由于点F(-2,3)在直线l:2x+y+1=0上,因此其轨迹为过点F(-2,3)且与直线l垂直的一条直线,故不正确;
③利用基本不等式的性质即可得出;
④将函数f(x)=sin(2x-
)的图象向右平移φ(>0)个单位后变为sin[2(x-φ)-
]=sin(2x-2φ-
)为偶函数,则2φ+
=kπ+
(k∈Z),即可得出φ的最小值;
⑤设P1(x1,y1),P2(x2,y2),P(x0,y0),则
+
=1,
+
=1,两式相减可得x0+2y0k1=0,k2=
,即可k1k2等于-
.
②由于点F(-2,3)在直线l:2x+y+1=0上,因此其轨迹为过点F(-2,3)且与直线l垂直的一条直线,故不正确;
③利用基本不等式的性质即可得出;
④将函数f(x)=sin(2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
⑤设P1(x1,y1),P2(x2,y2),P(x0,y0),则
| ||
| 2 |
| y | 2 1 |
| ||
| 2 |
| y | 2 2 |
| y0 |
| x0 |
| 1 |
| 2 |
解答:
解:①由函数f(x)=x
-(
)x,可知:函数在R上单调递增,因此最多有一个零点,而f(
)=(
)
-(
)
<0,f(
)=(
)
-(
)
>0,∴f(
)f(
)<0,因此函数的零点在区间(
,
)内,正确;
②由于点F(-2,3)在直线l:2x+y+1=0上,因此其轨迹为过点F(-2,3)且与直线l垂直的一条直线,故不正确;
③当a>0时,?x>0,不等式2x+
≥2
=2
≥4?a≥2,正确;
④若将函数f(x)=sin(2x-
)的图象向右平移φ(>0)个单位后变为sin[2(x-φ)-
]=sin(2x-2φ-
)为偶函数,则2φ+
=kπ+
(k∈Z),因此φ的最小值是
,正确;
⑤设P1(x1,y1),P2(x2,y2),P(x0,y0),则
+
=1,
+
=1,则
+(y1+y2)(y1-y2)=0,∴x0+2y0k1=0,k2=
,
∴k1k2等于-
,正确.
综上可得:①③④⑤正确.
故选:C.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
②由于点F(-2,3)在直线l:2x+y+1=0上,因此其轨迹为过点F(-2,3)且与直线l垂直的一条直线,故不正确;
③当a>0时,?x>0,不等式2x+
| a |
| x |
2x•
|
| 2a |
④若将函数f(x)=sin(2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
⑤设P1(x1,y1),P2(x2,y2),P(x0,y0),则
| ||
| 2 |
| y | 2 1 |
| ||
| 2 |
| y | 2 2 |
| (x1+x2)(x1-x2) |
| 2 |
| y0 |
| x0 |
∴k1k2等于-
| 1 |
| 2 |
综上可得:①③④⑤正确.
故选:C.
点评:本题考查了函数的单调性、函数零点的判定定理、抛物线的定义、基本不等式的性质、三角函数的图象变换、“点差法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
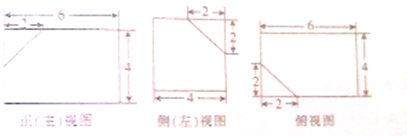
几何体的三视图如图,则该几何体的表面积为( )

A、122+
| ||
B、122+2
| ||
C、122+2
| ||
D、122+
|
设变量x、y满足
,则目标函数z=2x+3y的最小值为( )
|
| A、7 | B、8 | C、22 | D、23 |
程序框图如图所示:如果程序运行的结果S=1320,那么判断框中应填入( )


| A、K<10 | B、K≤10 |
| C、K<9 | D、K≤11 |