题目内容
已知无穷数列1,4,3,…
,…
(1)求这个数列的第10项
(2)
是这个数列的第n项
(3)这个数列有多少个整数项
(4)有否等于序号的
的项?若有,求出这些项,若没有,试说明理由
(5)从第几项开始,每一项与1的差的绝对值小于0.01.
| n+6 |
| n |
(1)求这个数列的第10项
(2)
| 53 |
| 50 |
(3)这个数列有多少个整数项
(4)有否等于序号的
| 1 |
| 3 |
(5)从第几项开始,每一项与1的差的绝对值小于0.01.
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:设无穷数列1,4,3,…
,…为{an}.
(1)a10=
即可得出.
(2)令
=
,解得n即可.
(3)由an=
=1+
,可得只有当n=1,2,3,6时,an为整数.
(4)假设
n=
,解得n即可.
(5)由|1+
-1|<0.01,解得n即可.
| n+6 |
| n |
(1)a10=
| 10+6 |
| 10 |
(2)令
| 53 |
| 50 |
| n+6 |
| n |
(3)由an=
| n+6 |
| n |
| 6 |
| n |
(4)假设
| 1 |
| 3 |
| n+6 |
| n |
(5)由|1+
| 6 |
| n |
解答:
解:设无穷数列1,4,3,…
,…为{an}.
(1)a10=
=
.
(2)令
=
,解得n=100,∴
是这个数列的第100项.
(3)∵an=
=1+
,∴只有当n=1,2,3,6时,an为整数,因此这个数列有4个整数项.
(4)假设
n=
,解得n=6,因此有等于序号的
的项,是第6项.
(5)由|1+
-1|<0.01,解得n>600.
∴从第600项开始,每一项与1的差的绝对值小于0.01.
| n+6 |
| n |
(1)a10=
| 10+6 |
| 10 |
| 8 |
| 5 |
(2)令
| 53 |
| 50 |
| n+6 |
| n |
| 53 |
| 50 |
(3)∵an=
| n+6 |
| n |
| 6 |
| n |
(4)假设
| 1 |
| 3 |
| n+6 |
| n |
| 1 |
| 3 |
(5)由|1+
| 6 |
| n |
∴从第600项开始,每一项与1的差的绝对值小于0.01.
点评:本题考查了数列的通项公式的应用及其性质,考查了计算能力,属于基础题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
程序框图如图所示:如果程序运行的结果S=1320,那么判断框中应填入( )


| A、K<10 | B、K≤10 |
| C、K<9 | D、K≤11 |
如图:程序输出的结果S=132,则判断框中应填( )


| A、i≥10? |
| B、i≤10? |
| C、i≥11? |
| D、i≥12? |
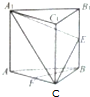 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.