题目内容
已知函数f(x)=x2-lnx-ax,a∈R.
(Ⅰ)当a=1时,求f(x)的最小值;
(Ⅱ)若f(x)>x,求a的取值范围.
(Ⅰ)当a=1时,求f(x)的最小值;
(Ⅱ)若f(x)>x,求a的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)当求函数的最值问题,利用求导,判断单调性,然后求极值,再判断最值;
(Ⅱ)求参数的取值范围,转化为求函数的最值问题.
(Ⅱ)求参数的取值范围,转化为求函数的最值问题.
解答:
解:(Ⅰ)当a=1时,f(x)=x2-lnx-x,
f′(x)=
.
当x∈(0,1)时,f′(x)<0;
当x∈(1,+∞)时,f′(x)>0.
∴f(x)的最小值为f(1)=0.
(Ⅱ)f(x)>x,即f(x)-x=x2-lnx-(a+1)x>0.
由于x>0,所以f(x)>x?x-
>a+1.
令g(x)=x-
,
则g′(x)=
.
当x∈(0,1)时,g′(x)<0;
当x∈(1,+∞)时,g′(x)>0.
g(x)有最小值g(1)=1.
故a+1<1,a的取值范围是(-∞,0).
f′(x)=
| (2x+1)(x-1) |
| x |
当x∈(0,1)时,f′(x)<0;
当x∈(1,+∞)时,f′(x)>0.
∴f(x)的最小值为f(1)=0.
(Ⅱ)f(x)>x,即f(x)-x=x2-lnx-(a+1)x>0.
由于x>0,所以f(x)>x?x-
| lnx |
| x |
令g(x)=x-
| lnx |
| x |
则g′(x)=
| x2-1+lnx |
| x2 |
当x∈(0,1)时,g′(x)<0;
当x∈(1,+∞)时,g′(x)>0.
g(x)有最小值g(1)=1.
故a+1<1,a的取值范围是(-∞,0).
点评:本题考查了导数与函数的最值问题,求参数的取值范围经常利用转化思想,转化为求最值的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
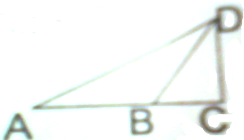 如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100
如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100